Элементы гидростатики

Чему в среднем равна гидростатика H2O?

Молекулярные частицы, собранные в некотором объеме, подвержены воздействию силы сжатия. Разные молекулы испытывают разное ГДВ. Это зависит от конкретного местоположения частиц в водном объеме. На поверхности сжатие меньше, на глубине, больше.

Вычислить значение ГДВ можно по формуле: P = pgh,

где:

• p – плотность воды (зависит от температуры, в округленном значении – 1 г/мл);
• g – значение ускорения свободного падения (9,8 м/сек²);
• h – глубина, где будет определяться давление.

Чтобы узнать среднее значение ГДВ для заданного объема, следует воспользоваться формулой:

Pср = P/S, где:

• P – гидростатическое давление, действующее на дно резервуара с водой;
• S – площадь дна емкости.

Задачи по гидростатике с решениями

Задача №1 на гидростатику

Условие

B кувшине с водой плавает кусок льда. Как изменится уровень воды в сосуде, когда лед растает? 

Решение

По условию плавания тел:

V – объем погруженной в воду части льда. После таяния льда образуется объем воды:

Как видим, объемы совпадают. Это значит, что при таянии льда его объем будет заменен таким же объемом воды.

Ответ: уровень не изменится.

Задача №2 на гидростатику

Условие

Кочан капусты массой 8 кг и объемом 10 л опускают в воду. Какой объем кочана окажется над водой?

Решение

Кочан плавает на поверхности, на него действуют сила Архимеда и сила тяжести:

Здесь V – объем кочана, погруженный в воду. Чтобы узнать объем кочана над водой, нужно из общего объема вычесть погруженный:

В одном кубическом метре – тысяча литров.

Ответ: 2 литра.

Задача №3 на гидростатику

Условие

Каково давление на дне озера глубиной 5 м? Атмосферное давление принять равным 100 кПа.

Решение

Вспоминаем основное уравнение гидростатики и записываем:

Ответ: 150 кПа.

Задача №4 на гидростатику

Условие

Вес тела в вакууме 2,6Н, в воде 1,6Н. Плотность воды 1000кг/м3. Определите плотность тела.

Решение

Вес – сила, с которой тело действует на опору. В воде вес меньше, так как на тело действует сила Архимеда, которая стремиться «поднять» его. В вакууме вес тела равен силе тяжести.

Ответ: 2600 кг/м3.

Задача №5 на гидростатику

Условие

Гидростатическое давление жидкости увеличилось в 5 раз. Как при этом изменилась высота столба жидкости в сосуде?

Решение

Формула для гидростатического давления:

Так как плотность жидкости и ускорение свободного падения остаются неизменными, можно сделать вывод, что высота столба жидкости увеличилась в пять раз.

Ответ: высота увеличилась в 5 раз.

Кстати! Для наших читателей действует скидка 10% на любой вид работы.

Закон Паскаля. Гидростатическое давление

Этот закон был открыт французским ученым Б. Паскалем в 1653 г. Его иногда называют основным законом гидростатики.

Закон Паскаля можно объяснить с точки зрения молекулярного строения вещества. В твердых телах молекулы образуют кристаллическую решетку и колеблются около своих положений равновесия. В жидкостях и газах молекулы обладают относительной свободой, они могут перемещаться друг относительно друга. Именно эта особенность позволяет давление, производимое на жидкость (или газ) передавать не только в направлении действия силы, но и во всех направлениях.

Закон Паскаля нашел широкое применение в современной технике. На законе Паскаля основана работа современных суперпрессов, которые позволяют создавать давления порядка 800 МПа. Также на этом законе построена работа всей гидроавтоматики, управляющей космическими кораблями, реактивными авиалайнерами, станками с числовым программным управлением, экскаваторами, самосвалами и т.д.

Гидростатическое давление жидкости

Гидростатическое давление внутри жидкости на любой глубине не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой определяется давление:

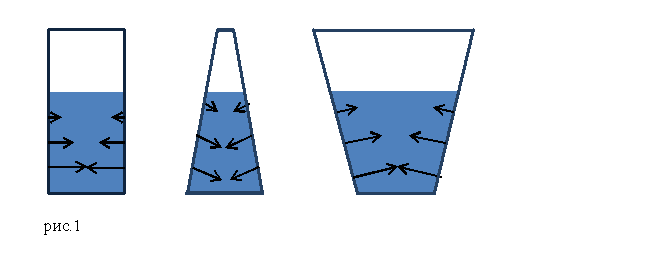
В однородной покоящейся жидкости давления в точках, лежащих в одной горизонтальной плоскости (на одном уровне), одинаковы. Во всех случаях, приведенных на рис. 1, давление жидкости на дно сосудов одинаково.

Рис.1. Независимость гидростатического давления от формы сосуда

На данной глубине жидкость давит одинаково по всем направлениям, поэтому давление на стенку на данной глубине будет таким же, как и на горизонтальную площадку, расположенную на такой же глубине.

Полное давление в жидкости, налитой в сосуд, складывается из давления у поверхности жидкости и гидростатического давления:

Давление у поверхности жидкости часто равно атмосферному давлению.

Несколько слов о кавитационном режиме насосов

При достижении определенных условий в насосах может возникать кавитация— явление, которое создается при снижении гидростатического давления и характеризуется появлением пузырьков газа в движущейся жидкости. В зоне, где гидростатическое давление повышается, пузырьки схлопываются.

В случае с лопастными насосами кавитацию чаще всего можно наблюдать в зоне потока максимальной скорости — вблизи входной кромки на лопатке рабочего колеса. Там, где пузырек схлопывается, резко увеличивается давление — если в момент схлопывания пузырек пара находится на поверхности лопатки или рабочего колеса, то удар воздействует на эту поверхность, что рано или поздно приведет к эрозии металла. Разрушение рабочих элементов лопастных насосов — самое опасное следствие кавитации. Кроме того, кавитация вызывает резкий шум техники, треск, вибрацию, может сопровождаться падением мощности, напора, подачи и КПД.

Сегодня не существует материалов, которые имели бы абсолютную устойчивость к кавитационным разрушениям, поэтому нельзя допускать работу насосов в кавитационном режиме. Основное средство по предупреждению кавитации — регулирование давления во всасывающем трубопроводе. Оптимальные параметры определяются высотой всасывания жидкости во время функционирования насоса.

Чтобы определить критический кавитационный запас, при производстве насоса проводят кавитационные испытания. В результате каждый режим работы насосного оборудования получает кавитационную характеристику, определяемую зависимостью мощности и напора насоса от кавитационного запаса.

дальнейшее чтение

• Бэтчелор, Джордж К. (1967). Введение в динамику жидкости . Издательство Кембриджского университета. ISBN 0-521-66396-2.
• Фалькович, Григорий (2011). Механика жидкости (Краткий курс для физиков) . Издательство Кембриджского университета. ISBN 978-1-107-00575-4.
• Kundu, Pijush K .; Коэн, Ира М. (2008). Гидромеханика (4-е изд.). Академическая пресса. ISBN 978-0-12-373735-9.
• Карри, И.Г. (1974). Фундаментальная механика жидкости . Макгроу-Хилл. ISBN 0-07-015000-1.
• Massey, B .; Уорд-Смит, Дж. (2005). Механика жидкостей (8-е изд.). Тейлор и Фрэнсис. ISBN 978-0-415-36206-1.
• Белый, Фрэнк М. (2003). Механика жидкости . Макгроу – Хилл. ISBN 0-07-240217-2.

Определение и основные понятия гидростатики

Определение

Раздел механики изучающий жидкости называют гидромеханикой.

Она в свою очередь делится на гидростатику и гидродинамику.

Определение

Гидростатика изучает состояния равновесия жидкостей и действие, которое оказывает жидкость на погруженные в нее тела.

Особенности жидкости, которые учитывает гидростатика:

• медленное изменение формы жидкости без изменения объема может протекать при воздействии бесконечно малой силы;
• в поле тяжести жидкость не имеет собственной формы, она принимает форму сосуда;
• поверхность жидкости в состоянии равновесия горизонтальна (перпендикулярна направлению силы тяжести) и это не зависит от формы сосуда;
• в сообщающихся сосудах жидкость одинаковой плотности находится на одном уровне.

Основной задачей гидростатики считают исследование проблемы распределения давления в жидкости и вычисления сил, действующих на тела, погруженные в вещество, зная это распределение.

Свойства

В каждой статичной жидкой среде всегда присутствует напряжение сжатия. К примеру, вода, размещенная в условном баке, станет давить на его стенки и дно. А если погрузить в воду какой-либо предмет, то можно с уверенностью сказать, что этот предмет окажется под воздействием силовой нагрузки.

К основным свойствам гидростатического давления относят три закономерности:

1. ГДВ всегда направлено перпендикулярно той площадке, на которую оно оказывает действие. Стенки емкостей бывают вертикальными, бывают наклонными. На направление действия силы это совершенно не влияет. Давление внутри емкости все равно будет направлено под углом 90° к стенкам.
2. В любой точке жидкости величина ГДВ неизменна по всем направлениям. Свойство №2 объясняется молекулярным строением воды. Частицы в жидкостях довольно свободны, и способны легко перемещаться относительно друг друга. У твердых материалов молекулы собраны в кристаллические решетки, поэтому их форма неизменна.

   Из этого обстоятельства следует, что когда давление распространяется на конкретный объем воды, в котором молекулы не имеют прочных связей, то оно одинаково действует во все стороны. При этом сила этого давления имеет одну и ту же величину.

3. ГДВ в некоторой точке будет зависеть от ее месторасположения в пространстве. Это свойство очевидно. Вполне понятно, что чем глубже тело опустится в жидкую среду, тем больше окажется показатель ГДВ. И, наоборот, при незначительном погружении, ГДВ будет маленьким.

Определение закона Паскаля

Итак, мы подошли к формулировке закона Паскаля, и звучит она так:

Давление, производимое на жидкость или газ, передается в любую точку одинаково во всех направлениях.

Обратите внимание — закон работает только с жидкостями и газами. Дело в том, что молекулы жидких и газообразных веществ под давлением ведут себя совсем не так, как молекулы твердых тел

Если молекулы жидкости и газа движутся почти свободно, то молекулы твердых тел так не умеют. Они могут лишь колебаться, немного отклоняясь от исходного положения. Именно благодаря свободному передвижению молекулы газа и жидкости оказывают давление во всех направлениях.

Рассмотрим опыт с шаром Паскаля, чтобы стало понятнее.

Присоединим к трубе с поршнем полый шар со множеством небольших отверстий. Зальем в шар воду и будем давить на поршень. Давление в трубе вырастет и вода будет выливаться через отверстия, причем напор всех струй будет одинаковым. Такой же результат получится, если вместо воды в шарике будет газ.

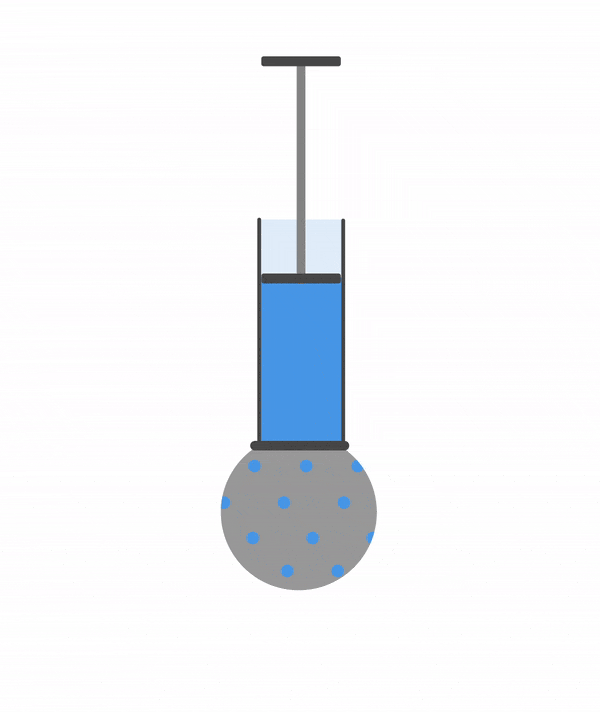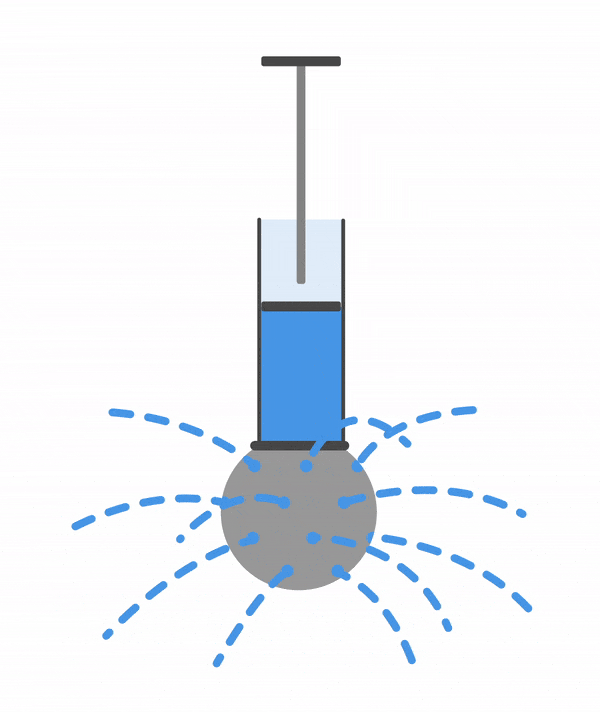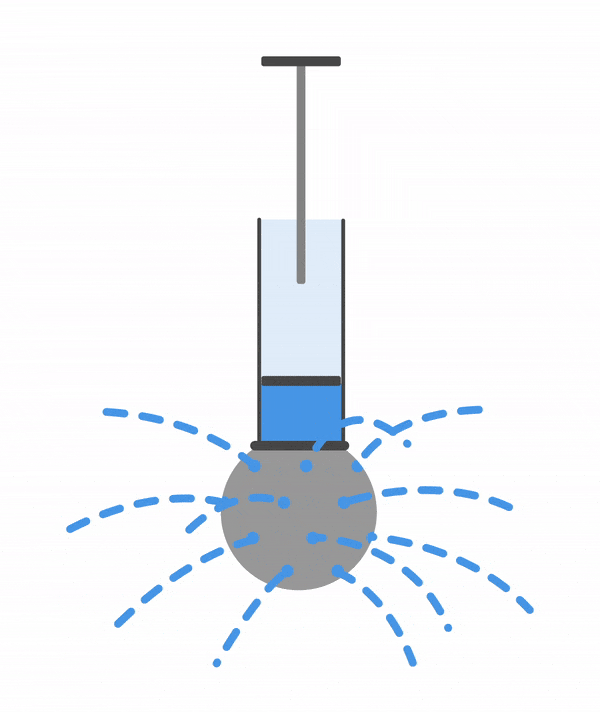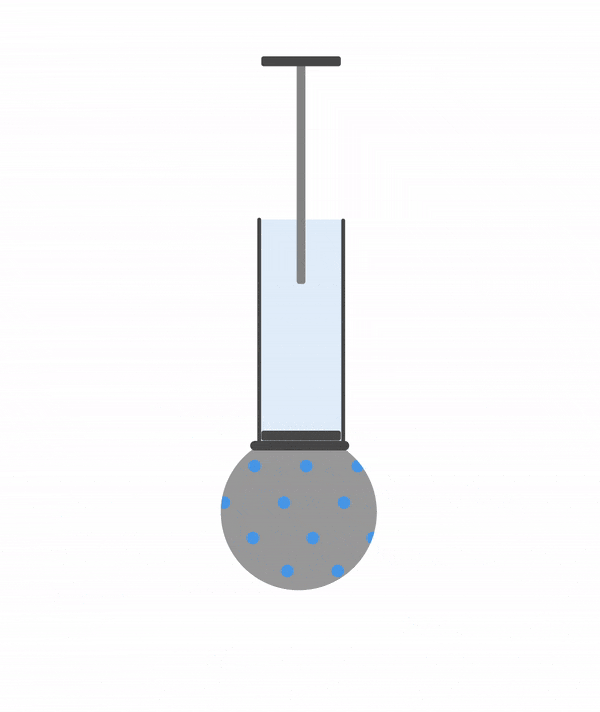Важный момент
У Земли есть атмосфера. Эта атмосфера создает давление, которое добавляется ко всем другим. То есть если мы давим рукой на стол, то давление, которое испытывает стол — это давление нашей руки плюс атмосферное.

Как определить?

Узнать ГДВ в требуемой точке возможно с помощью уравнения, которое называется: основное уравнение гидростатики. Выражено оно в виде:

 P = P0 + yh,

где:

• P0 – давление на внешней поверхности жидкости (атмосферное);
• y – удельный вес воды;
• h – высота водного столба (глубина).

Показательно, что ГДВ в заданной точке будет равно величине, состоящей из суммы значений: вес атмосферного столба и вес водного слоя. Наименование у этого параметра – полное давление.

Если на водную поверхность давит сила, которая больше атмосферной нагрузки, то такой вид воздействия будет именоваться, как избыточное давление. Он выражается разностью между полным и атмосферным давлением:

 Pизб = Pполн — Pатм

Пояснительным примером может послужить компрессор холодильника, который создает избыточное сжатие  газа в герметичной камере.

История

Некоторые принципы гидростатики были известны в эмпирическом и интуитивном смысле с древних времен строителям лодок, цистерн , акведуков и фонтанов . Архимеду приписывают открытие принципа Архимеда , который связывает силу плавучести на объекте, погруженном в жидкость, с весом жидкости, вытесняемой объектом. Римский инженер Витрувий предупреждал читателей о свинцовых труб трещит под гидростатическим давлением.

Понятие давления и того, как оно передается жидкостями, было сформулировано французским математиком и философом Блезом Паскалем в 1647 году.

Гидростатика в Древней Греции и Риме

Кубок Пифагора

«Чаша ярмарки» или чаша Пифагора , датируемая примерно 6 веком до нашей эры, представляет собой гидравлическую технологию, изобретение которой приписывают греческому математику и геометру Пифагору. Его использовали как инструмент обучения.

Чашка состоит из линии, вырезанной внутри чашки, и небольшой вертикальной трубы в центре чашки, ведущей к дну. Высота этой трубы такая же, как линия, вырезанная внутри чашки. Стакан может быть заполнен до линии без прохождения жидкости в трубу в центре стакана. Однако, когда количество жидкости превышает эту линию заполнения, жидкость будет перетекать в трубу в центре чашки. Из-за сопротивления, которое молекулы оказывают друг на друга, стаканчик опустеет.

Фонтан цапли

Фонтан Герона — это устройство, изобретенное Героном Александрийским, которое состоит из струи жидкости, питаемой резервуаром с жидкостью. Фонтан устроен таким образом, что высота струи превышает высоту жидкости в резервуаре, очевидно, в нарушение принципов гидростатического давления. Устройство состояло из отверстия и двух емкостей, расположенных друг над другом. Промежуточный сосуд, который был запечатан, был заполнен жидкостью, и несколько канюль (небольшая трубка для передачи жидкости между сосудами) соединяли различные сосуды. Захваченный воздух внутри сосудов вызывает струю воды из сопла, сливая всю воду из промежуточного резервуара.

Паскаль внес вклад в развитие как гидростатики, так и гидродинамики. Закон Паскаля — это фундаментальный принцип механики жидкости, который гласит, что любое давление, приложенное к поверхности жидкости, передается равномерно по жидкости во всех направлениях, так что начальные изменения давления не меняются.

Давление

Идущий по рыхлому снегу человек будет в него постоянно проваливаться. А вот на лыжах он сможет передвигаться по тому же самому снегу спокойно. Казалось бы, ничего не меняется — человек воздействует на снег с одинаковой силой и на лыжах, и без них.

Дело в том, что «проваливание» в снег характеризуется не только силой — оно также зависит от площади, на которую эта сила воздействует. Площадь поверхности лыжи в 20 раз больше площади поверхности подошвы, поэтому человек, стоя на лыжах, действует на каждый квадратный сантиметр с силой в 20 раз меньшей, чем без них.

Или, например, если вы будете с одинаковой силой втыкать кнопки в пробковую доску, легче войдет та кнопка, у которой более заостренный конец, так как его площадь меньше.

Резюмируем: результат действия силы зависит не только от ее модуля, направления и точки приложения, но и от площади поверхности, к которой эта сила приложена.

А теперь подтвердим этот вывод опытами, как настоящие физики.

Возьмем небольшую доску и вобьем гвозди в ее углы. Также возьмем емкость с песком и поставим конструкцию из доски и гвоздей в эту емкость. Сначала расположим конструкцию шляпками вниз и поставим на нее гирю. Конструкция не утонет в песке, а только чуть-чуть углубится в него.

Затем перевернем конструкцию так, чтобы шляпки гвоздей оказались сверху и также поставим на доску гирю. Теперь конструкция утонет в песке.

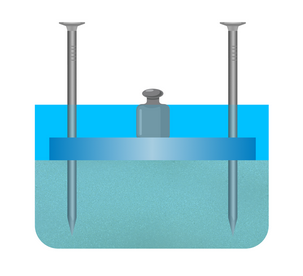
От того, какая сила действует на каждую единицу площади поверхности, зависит результат действия силы.

Во всех примерах мы говорили о действии силы, перпендикулярной поверхности. Чтобы охарактеризовать это действие, используется величина давление.

Давление p = F/S p — давление F — сила S — площадь

Гидростатика.

Давление — скалярная физическая величина, равная отношению модуля силы, действующей перпендикулярно поверхности, к площади её поверхности.   

Гидростатическое давление — давление, обусловленное весом столба жидкости. Манометр — прибор для измерения давления в жидкости или газа. 

p = ρ_жgh   — давление на произвольной глубине несжимаемой жидкости            

F = pS = ρ_жghS_дна  — сила давления на дно сосуда         

 На одном и том же уровне давление одинаково во всех направлениях.

Давление р на произвольной глубине h сжимаемой поршнем жидкости определяется давлением поршня и давлением столба жидкости           р = р_порш. + ρ_жgh

 Атмосферное давление – давление, которое производит воздушная оболочка Земли.

Опыт Торричелли (1634 г.) свидетельствует: атмосферное  давление  равно давлению столба ртути в трубке.

Нормальное атмосферное давление:  1 атм = 760 мм.рт.ст. = 1 01325 Па ≈ 105 Па (при 0ºС);     1 мм.рт.ст.=133,3 Па

Оно может изменяться от места к месту и во времени (циклоны и антициклоны) и убывает с увеличением высоты над уровнем моря (на каждые 12 м подъёма  оно уменьшается на 1 мм. рт. ст.).

Барометры — приборы для измерения атмосферного давления. Существуют 1) жидкостный;  2) барометр — анероид (металлический).

Закон Паскаля (1653 г.) —  жидкости и газы передают производимое на них давление во все стороны одинаково. 

 Сообщающимися называются сосуды, соединённые между собой каналом с жидкостью.

Закон Архимеда: на тело, погруженное в покоящуюся жидкость (или газ), действует выталкивающая сила, направленная  вертикально верх и равная весу жидкости, вытесненной телом.

F_A =ρ_жgV_пчт                        F_A = Р_ж,выт.= m_ж,выт g,

F_A = Р_воз — Р_жид.    V_пчт – объём погруженной части тела.    ρ_ж — плотность жидкости или газа.

Условие плавания тел

а) F_A > mg, ρ_т > ρ_ж— тело всплывает;  

б) F_A < mg, ρ_т < ρ_ж — тело тонет;      

в) F_A = mg, ρ_т = ρ_ж — тело находится в равновесии на любой глубине.  

Условие плавания тела на поверхности  F_A = mg

Если тело будет плавать частично погрузившись в жидкость, то ρ_ж/ρ_т=V_т/V_пчт

На этом основано применение ареометра- прибора для определения плотности жидкости.

Статика и гидростатика. Шпаргалка

1 файл(ы) 491.16 KB

Конспект урока «Статика и гидростатика. Теория и формулы для ЕГЭ» + шпаргалка.

Еще конспекты для 10-11 классов:

СТАТИКА И ГИДРОСТАТИКА Теория и формулы (кратко)

Статика — раздел механики, изучаю­щий условия равновесия тел.

Условия рав­новесия  тела:

а) Поступательно движущееся тело на­ходится в состоянии равновесия (покоится или движется прямолинейно и равномерно),    если 

б) Вращающееся    тело,   имеющее   непо­движную ось вращения, находится в покое или равномерно вращается, если         М₁ + М₂ + М₃ + … + M_N = 0,  где М — момент силы —  произведение силы на её плечо.

Виды равновесия.

1. Виды равновесия тела с закрепленной осью вращения

а) если ось проходит через центр масс, то тело находится в безразличном равновесии при любом положении тела (а);

б) ось выше точки центра тяжести — ус­тойчивое равновесие (б);

в) ось ниже точки центра тяжести — неус­тойчивое равновесие( в).

1. Виды равновесия тела, имеющего точ­ку опоры:

а) если равнодействующая всех сил направлена к положению равновесия, то тело нахо­дится в устойчивом положении (рис. а);

б)    если равнодействующая всех сил направлена от положения равновесия, то тело находится в неустойчивом  равновесии (рис. б);

в)    если Σ  = 0, — равновесие безразличное (рис. в).

1. Виды равновесия тела, имеющего пло­щадь опоры.

Если вертикаль, проведенная через центр тяжести тела, пересекает площадь его опоры, то равновесие тела устойчивое. Если не пересекает, то тело падает, — равновесие не­устойчивое.

Простые механизмы и блоки

Простые механизмы — приспособления, которые служат для преобразования силы. К ним относятся:  рычаг (блок, ворот) и наклонная плоскость (клин, винт). Они применяются для получения выигрыша в силе.

F₂/F₁ – выигрыш в силе.      F₁l₁=F₂l₂ — условие равновесия рычага для двух сил.

Золотое правило механики: все простые механизмы, не дают выигрыша в работе — во сколько раз мы выигрываем в силе, во столько же раз мы проигрываем в расстоянии.

Определение гидростатического давления

Определение

Физическая величина, равная отношению нормальной силы ($F$), действующей со стороны жидкости на некоторую площадь,
на величину этой площади ($S$) называют давлением ($p$) жидкости:

\

Если несжимаемая жидкость находится в равновесии давление по горизонтали всегда одно и то же. Свободная поверхность жидкости всегда горизонтальна, за исключением места около стенок сосуда. У несжимаемой жидкости плотность не зависит от давления. Если поперечное сечение цилиндрического столба жидкости равно $S$, высота столба $h$, плотность жидкости $\rho $, тогда вес ($P$) этого столба равен:

В соответствии с (1) давление на основание столба жидкости составит величину:

Формула (3) указывает, что давление столба несжимаемой жидкости на дно сосуда зависит от высоты и плотности жидкости.
В общем случае плотность зависит от температуры жидкости. Давление, которое вычисляется при помощи формулы (3)
называют гидростатическим давлением/

Определение

И так, гидростатическим давлением называют давление столба жидкости, находящейся в состоянии равновесия, над некоторым
условно выбранным уровнем при действии силы тяжести. Гидростатическое давление определяется по формуле (3).

Давление внутри жидкости ($p$) на глубине $h$, будет складываться из давления атмосферы ($p_0$) и гидростатического давления:

Единицей измерения гидростатического давления в Международной системе единиц (СИ) является паскаль (Па):

Примеры задач с гидростатическим давлением

Пример 1

Задание. В чем состоит суть гидростатического парадокса?

Решение. Гидростатическим парадоксом называют явление, при котором сила весового давления жидкости, находящейся в сосуде отличается от веса находящейся там жидкости. Сила давления жидкости на дно емкости равняется весу жидкости только в том случае, если сосуд имеет форму цилиндра. При такой конфигурации емкости стенки являются вертикальными, силы давления стенок на жидкость (соответственно, жидкости на стенки) направлены горизонтально, вертикальной составляющей они не имеют (рис.1).

Если сосуд имеет вверху поперечное сечение больше, чем сечение дна, то сила давления на дно меньше, чем вес жидкости. И наоборот, если сосуд с жидкостью имеет сужающееся вверху горло, то сила давления на дно сосуда больше, чем вес жидкости. Причиной возникновения гидростатического парадокса является то, что жидкость оказывает давление не только на дно сосуда, но давит и на его стенки. При этом давление на стенки сосуда, расположенные не перпендикулярно основанию имеют вертикальную составляющую. При этом в сосуде, который расширяется к верху, эта составляющая направлена вверх, а в сосуде, уменьшающем свое сечение к верху, вертикальная составляющая давления направлена вниз. Вес жидкости вычисляется как сумма всех вертикальных компонент давления жидкости по внутренней площади емкости.

   

Пример 2

Задание. Каково гидростатическое давление воды на дно сосуда с водой, если высота столба жидкости составляет $h=$0,5 м?

Решение. Гидростатическое давление на дно сосуда найдем как:

\

где $\rho =1000\ \frac{кг}{м^3}$.

Вычислим это давление:

\

Ответ. $p\approx 5000$ Па

Закон Архимеда

Вследствие разности давлений в жидкости на разных уровнях появляется архимедова сила F_formula__А или сила выталкивающая.

Возникновение выталкивающей силы поясним на рисунке 1.15.3.

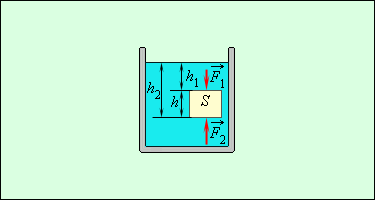
Рис. 1.15.3. Архимедовасила. FА=F2–F1=S(p2–p1)=ρgSh, F1=p1S, F2=p2S.

Прямоугольный параллелепипед (h – высота, S – площадь основания) погрузим в жидкость. Запишем разность давлений на нижнюю и верхнюю грани: Δp=p2–p1=ρgh. Таким образом, выталкивающая сила FА будет иметь направление вверх, и ее модуль: FА=F2 – F1=SΔp=ρgSh=ρgV (V является объемом вытесненной жидкости; ρV– ее массой).

Определение 5

Закон Архимеда: архимедова сила, оказывающая воздействие на тело, погруженное в жидкость или газ, равна весу жидкости или газа, который вытесняется телом.

Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!

Описать задание

Закон Архимеда применим к телам любой формы.

Следствием из закона Архимеда является утверждение, что, если средняя плотность тела ρт больше плотности жидкости (или газа) ρ, тело опустится на дно. Если же ρт<ρ, тело будет плавать на поверхности жидкости. Объем той части тела, которая погружена в жидкость, будет таким, что вес вытесненной жидкости станет равным весу тела. Чтобы поднять воздушный шар в воздух, его вес должен быть меньше, чем вес вытесненного воздуха. Именно по этой причине воздушные шары наполняют легкими газами (водородом, гелием) либо нагретым воздухом.

Мы получили выше формулу, определяющую полное давление в жидкости p=p+ρgh; из нее следует, что в сообщающихся сосудахлюбой формы, наполненных однородной жидкостью, давления в любой точке на одном и том же уровне одинаковы (рис. 1.15.4).

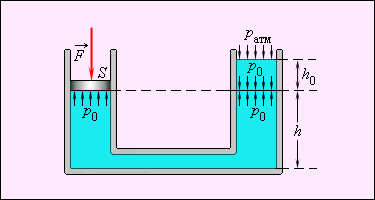
Рис. 1.15.4. Пример сообщающихся сосудов. В правом сосуде поверхность жидкости свободна. На уровне h давление в обоих сосудах одинаково и равно p=FS=ρgh+pатм. Давление на дно сосудов p=p+ρgh.

Закрыв поршнями оба цилиндра вертикального расположения сообщающихся сосудов и приложив внешнюю силу к поршням, мы создадим в жидкости большое давление p, во много раз превышающее гидростатическое давление ρgh в любой точке системы. В таком случае можно утверждать, что во всей системе установлено одинаковое давление p.

При разных площадях поршней (S1 и S2) и воздействие на них силы со стороны жидкости будет разным (F1=pS1 и F2=pS2). Для удержания системы в состоянии равновесия прикладываемые силы к поршням должны быть такими же по модулю, но имеющими противоположную направленность. В итоге имеем: F1S1=F2S2 или F2=F1S2S1.

Если S2≫S1, то F2≫F1. Устройства такого строения дают возможность использовать значительный выигрыш в силе и называются гидравлическими машинами (рис. 1.15.5). При перемещении поршня в узком цилиндре вниз под воздействием внешней силы F1 на расстояние h1 поршень в широком цилиндре сдвинется на расстояние h2=S1S2h1, поднимая тяжелый груз.

Из всего сказанного следует:

Определение 6

«Золотое правило механики»: выигрыш в силе в n=S2S1 раз всегда соответствует такому же проигрышу в расстоянии, а произведение силы при этом не изменяется: F1h1=F2h2.

Данное правило справедливо для всех идеальных машин, в которых исключена сила трения.

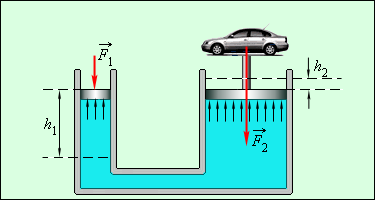
Рис. 1.15.5. Гидравлическая машина.

Определение 7

Гидравлические машины, используемые для подъема грузов, называют домкратами.

Домкраты широко применяются, в том числе, в качестве гидравлических прессов. В качестве жидкости обычно используют минеральные масла.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Большая Энциклопедия Нефти и Газа

Основной закон гидростатики, согласно которому давление, создаваемое в любой точке покоящейся несжимаемой жидкости, одинаково во всех точках ее объема.  

Основной закон гидростатики — это закон Паскаля, согласно которому в состоянии равновесия величина давления р в жидкости ( или газе) не зависит от ориентации площадки, на которую оно действует.  

Основной закон гидростатики широко применяется для решения практических задач

Однако при его использовании в практических расчетах следует обращать особое внимание на высоту / г, так как она может принимать как положительные, так и отрицательные значения.  

Кроме основных законов гидростатики Архимеда, Сте-вин формулирует еще два положения, касающиеся элементарных свойств несжимаемой тяжелой жидкости.  

Как записывается основной закон гидростатики.  

ПАСКАЛЯ ЗАКОН — основной закон гидростатики, согласно к-рому давление, производимое внешними силами на поверхность жидкости, передается одинаково по всем направлениям.  

ПАСКАЛЯ ЗАКОН — основной закон гидростатики, согласно к-рому давление на поверхность жидкости, произведенное внеш.  

Полученное уравнение называют основным законом гидростатики. Оно позволяет подсчитать давление в любой точке внутри покоящейся жидкости.  

Это уравнение и выражает основной закон гидростатики.  

При выборе знака в основном законе гидростатики всегда следует помнить, что чем ниже ( глубже) располагается точка в данной жидкости, тем больше давление в этой точке.  

Гидравлический пресс.| Сосуды разной формы.

Это и есть принцип Паскаля — основной закон гидростатики.  

В заключение следует добавить, что основной закон гидростатики широко используется при измерении давлений.  

Схема действия сил при прямолинейном движении сосуда.

Эта зависимость является более общей, чем основной закон гидростатики, который может быть получен из нее как частный случай. Тогда с учетом 1 Низ (2.11) получим формулу (2.1), т.е. основной закон гидростатики.  

Страницы:      1    2    3

Заключение

Гидростатическое давление воды – это очень важный показатель. Он позволяет производить не только расчеты при разработке и производстве различных устройств, работающих на основе законов гидростатики.

Его часто задействуют и простые люди, на самом обычном бытовом уровне, даже не подозревая об этом. Например, используя прибор для измерения артериального давления, или включая насос на даче.

Три свойства, которыми обладает гидростатика воды, остаются неизменными при любых обстоятельствах, что полезно помнить. Ведь при необходимости, можно даже самостоятельно произвести какие-либо математические расчеты. Например, вычислить ГДВ на дне моря или океана.