Какая физическая величина является силовой характеристикой магнитного поля

Свойства силовых линий электростатического поля

Можно выделить два свойства силовых линий поля, создаваемого неподвижными зарядами:

1. Силовые линии имеют начало и конец – они начинаются на положительных и заканчиваются на отрицательных зарядах.
2. Напряженность поля больше в той области, в которой линии располагаются гуще.

Рис. 15. Два свойства силовых линий электрического поля, созданного неподвижными зарядами

Примечание: Существует, так же, вихревое электрическое поле. Это поле не связано с неподвижными зарядами. Его линии замкнуты сами на себя. Картина такого поля представляет собой нечто похожее на вихрь, отсюда и появилось его название. Подробнее о вихревом электрическом поле написано в статье, посвященной электромагнитным волнам.

Где заканчиваются линии единственного заряда

Линии электростатического поля, начавшись на положительном заряде, должны закончиться на каком-либо отрицательном заряде.

Если поблизости от какого-либо заряда не располагается второй заряд, имеющий противоположный знак, то линии поля такого одинокого заряда уходят в бесконечность.

Там, далеко, на бесконечности, всегда найдется заряд, имеющий противоположный знак, на котором будут заканчиваться линии рассматриваемого одиночного заряда.

Рис. 16. Если заряд единичный и поблизости других зарядов противоположного знака нет, то силовые линии его уходят в бесконечность и там заканчиваются на противоположном заряде

Силовая характеристика

Силовую характеристику электрического поля определяет его напряженность.
 

Силовой характеристикой поля является его напряженность, в данном случае сила, отнесенная к единице массы тела и равная ускорению g его свободного падения.
 

Силовой характеристикой магнитного поля является вектор магнитной индукции В. Его удобно определять по ориентирующему действию магнитного поля на маленький контур с током 7 и площадью S, внесенный в данную точку поля. Характеристикой контура является величина рт IS — магнитный момент контура с током. Для плоского контура с током вектор рт расположен перпендикулярно плоскости контура и связан с направлением тока / правилом правого винта.
 

Силовой характеристикой гравитационного поля является его напряженность, измеряемая силой, действующей на материальную точку единичной массы.
 

Силовой характеристикой магнитного поля является индукция В. Эта векторная физическая величина обычно вводится путем рассмотрения действия магнитного поля на маленькую пробную рамку с током. Направление вектора В совпадает с направлением нормали к свободной пробной рамке с током, установившейся в поле.
 

Силовой характеристикой электрического поля является его напряженность. С помощью величины напряженности представляется возможным оценивать интенсивность электрического поля и определять силу, действующую со стороны поля на заряженную частицу.
 

Силовой характеристикой регулирующего органа называется зависимость изменения необходимого перестановочного усилия от перемещения затвора.
 

Силовой характеристикой магнитного поля является индукция В. Как и электрическое поле, магнитное удовлетворяет принципу суперпозиции.
 

Если силовая характеристика выражается многочленом более высокой степени, чем вторая, то спектр деформации будет еще богаче высшими составляющими и комбинационными тонами.
 

Если силовые характеристики основного упругого элемента и ограничителей хода линейны, то общая характеристика принимает вид ломаной ( фиг. Следовательно, система в целом оказывается нелинейной; к ней приложимы выводы и методы расчета, приведенные в общем виде в гл.
 

Зависимости режимного параметра ( а и осевой жесткости ( б от безразмерной нагрузки для уплотнения с питающими отверстиями и камерами ( Ьу. г при работе в газе..

Расчеты силовых характеристик ввиду сложности формул обычно выполняют с помощью ЭВМ.
 

Герметичный насос, гидростатические подшипники которого питаются лабиринтными насосами.

Жесткость силовой характеристики пят зависит от жесткости гидравлических характеристик H ( Q) дросселирующих кольцевых щелей и лабиринтного насоса.
 

4.Понятие о циркуляции

Пусть в некоторой области пространства существует векторное поле .

Циркуляцией вектора  по произвольному замкнутому контуру L называется следующий криволинейный интеграл:

Здесь  — единичный вектор, касательный к контуру в данной точке, направленный в сторону положительного обхода контура.

Существует соглашение, что положительное направление обхода контура (направление ) выбирается таким, чтобы область, охваченная
контуром, оставалась при обходе слева.

Напомним, вкратце, как можно “сконструировать” криволинейный интеграл. Для этого нужно
выбрать точку на контуре, показать в ней вектор , в этой же точке показать единичный вектор
касательной, вычислить скалярное произведение , разбить контур на малые элементы, длину элемента обозначить , вычислить произведение ; проделать это для всех элементов контура; произвести суммирование результатов,
устремляя элемент длины контура  к нулю — перейти от суммирования к интегрированию.

Так же, как и поток, циркуляция является ещё одной характеристикой свойств векторного поля. А именно, циркуляция характеризует
степень завихренности векторного поля.

Пример: если в качестве «измерителя» циркуляции поля скоростей жидкости можно взять турбинку, то если она вращается, циркуляция не равна нулю.

Циркуляция – это интегральная характеристика поля.

Электрическое поле. ЗАДАЧИ с решениями

Формулы, используемые на уроках по теме «Электрическое поле. ЗАДАЧИ» в 10-11 классах при подготовке к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Электрон движется без начальной скорости вдоль силовой линии однородного электрического поля напряженностью Е = 2 • 104 Н/Кл. Какой путь S он пролетит прежде, чем его скорость станет v = 100 км/с ? Среда — воздух. Модуль заряда электрона е = 1,6 • 10–19 Кл, его масса m_e = 9,1 • 10–31 кг.

Задача № 2.
 Пылинка с зарядом q = 1 нКл неподвижно висит в однородном электрическом поле напряженностью Е = 2 • 104 Н/Кл, вектор напряженности которого направлен вверх (рис. 2-9). Найти массу пылинки т. Сколько избыточных электронов N содержит пылинка? 

Задача № 3.
 Заряженный шар диаметром D находится в равновесии в жидком диэлектрике плотностью р₁ с диэлектрической проницаемостью ε (рис. 2-10). Найти поверхностную плотность зарядов на шаре σ, если плотность вещества шара р₂. Напряженность электрического поля в диэлектрике Е, вектор напряженности направлен вверх. 

Задача № 4.
На каком расстоянии г₂ от точечного заряда напряженность электрического поля этого заряда в жидком диэлектрике с диэлектрической проницаемостью ε₂ = 81 (вода) такая же, как на расстоянии r₁ = 9 см от этого заряда в воздухе?

Задача № 5.
 Электрон влетает в однородное электрическое поле со скоростью v, направленной перпендикулярно вектору напряженности Е (рис. 2-11). Под каким углом φ к линиям вектора напряженности будет направлен вектор его скорости через время t полета в поле? Чему будет равна работа сил поля А за это время? Чему будет равна кинетическая энергия электрона W_кчерез время t ? Напряженность поля Е. Масса электрона т_еи его заряд е известны. 

Задача № 6.
 Тонкая металлическая пластинка массой m падает вертикально вниз равноускоренно так, что ее плоскость остается горизонтальной. Падению пластинки противодействует сила сопротивления среды F_соnp. Найти напряженность электрического поля Е, возникающего внутри пластинки вследствие инерции свободных электронов. Масса электрона m_e, его заряд е.

Задача № 7.
 К бесконечной, вертикальной, равномерно заряженной плоскости прикреплена одним кондом невесомая нить, на другом конце которой находится одноименно с нитью заряженный шарик радиусом R = 0,5 см, несущий заряд q = 1 • 10–10 Кл. Плотность вещества шарика р = 2 • 103 кг/м3. Натяжение нити F_н = 4,9 • 10–2 Н. Какой угол а образует с плоскостью нить, на которой висит шарик (рис. 2-12)? Среда – воздух. Чему равна поверхностная плотность σ зарядов на плоскости? 

Задача № 8.
 Сфера радиусом R = 1 см равномерно заряжена. Поверхностная плотность зарядов на сфере σ = 10 нКл/см2. Найти напряженность Е₁ электрического поля на расстоянии r₁ = 10 см от центра сферы (рис. 2-13). Построить график зависимости напряженности Е от расстояния r в пределах от r = 0 до r₁ = 10 см. Среда — воздух. 

Задача № 9.
 Заряды q₁ = 20 нКл и q₂ = 10 нКл расположены на расстоянии r = 10 см друг от друга. Найти напряженность электрического поля Е₁, созданного этими зарядами в точке 1, расположенной на расстоянии r₁ = 4 см от заряда q₁ и напряженность Е₂ в точке 2, расположенной на расстоянии г₂ = 2 см от заряда q₂ (рис. 2-15). Среда — вакуум. 

Задача № 10.
 Два одноименных точечных заряда q и 4q расположены на расстоянии r друг от друга. На каком расстоянии r₁ от заряда q находится точка М, в которой напряженность поля этих зарядов Е = 0? На каком расстоянии r₂ от заряда q находится такая точка, если эти заряды разноименные?

Задача № 11.
 На расстоянии г = 3 см от поверхности шара радиусом R = 2 см находится точечный отрицательный заряд q = –2 нКл. Шар заряжен положительно с поверхностной плотностью зарядов σ = 2 нКл/м2. Найти напряженность поля Е, созданного заряженным шаром и точечным зарядом, в точке, расположенной на расстоянии r₁ = 4 см от центра шара, и г₂ = 3 см от заряда q. Среда — воздух.

Задача № 12.
 В вершинах равностороннего треугольника со стороной а находятся заряды q, –q и q. Найти напряженность поля Е, созданного этими зарядами в центре треугольника. Среда — воздух.

(с) В учебных целях использованы цитаты из учебного пособия «Новый репетитор по физике для подготовки к ЕГЭ : задачи и методы их решения / И.Л. Касаткина; под ред. Т.В. Шкиль. — Ростов н /Д : Феникс».

Это конспект по теме «Электрическое поле. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

§ 54. Электрическое поле внутри проводника с током

В проводниках тока имеется большое количество хаотически движущихся свободных заряженных частиц — электронов, ионов. Если эти частицы заставить помимо хаотического движения еще двигаться в целом в виде направленного потока, то получится электрический ток. В электрических цепях частицы, образующие тек, приводятся в направленное движение электрическим полем, которое создает источник тока в проводах цепи вследствие наличия на его полюсах разности потенциалов. Электрическое поле внутри и вокруг неподвижного проводника с постоянным током называется стационарным электрическим полем.

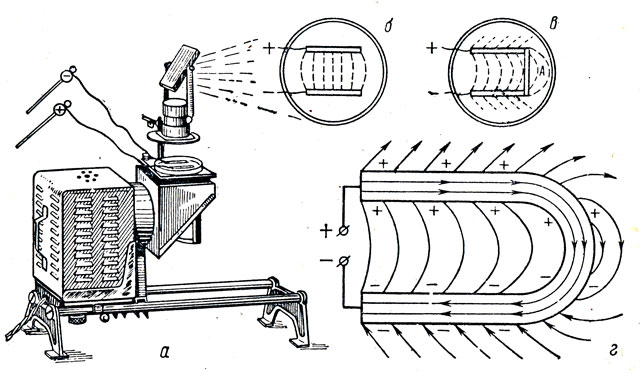Рис. 72. Линии напряженности стационарного электрического поля

Наблюдать такое поле можно на следующем опыте. В проекционной ванночке имеется тонкий слой прозрачного жидкого диэлектрика, в котором находятся мелко нарезанные волоски и две параллельные влажные палочки (рис. 72, а). Присоединим проводники (палочки) к источнику напряжения (к шарикам электрофорной машины). Волоски приходят в движение и располагаются, создавая картину электростатического поля заряженных проводников, в котором линии напряженности нормальны к поверхности проводников (рис. 72, б). Замкнем цепь в ванночке деревянной палочкой А (рис. 72, в). В проводнике и вокруг него образуется стационарное электрическое поле. Под его действием возникает ток, и вид прежнего поля изменяется. Сравнивая картину электростатического и стационарного полей, видим, что* между ними есть отличие:

1. Линии напряженности электростатического поля заряженного проводника перпендикулярны к поверхности проводника, а стационарного поля вне проводника — наклонны в направлении тока (рис. 72, г). Обнаружить стационарное электрическое поле вне проводника такими приемами, как обнаруживается электростатическое поле зарядов гильзой, нельзя из-за малой напряженности первого. Внутри прямолинейного проводника стационарное поле однородное (его линии напряженности направлены вдоль проводника), внутри криволинейного — неоднородное.
2. В любой точке стационарного поля есть напряженность, на что указывает наличие тока в цепи.

3. Потенциал поля внутри проводника и на его поверхности уменьшается в направлении движения тока. В этом можно убедиться на таком опыте (рис. 73). Приведя в действие электрофорную машину, получим в цепи из шпагата (потертого влажной тряпочкой) электрический ток. Начнем электрометр, соприкасающийся стержнем, со шпагатом, передвигать вдоль цепи. Видим, что потенциал в разных точках цепи различен. У шарика А он был наибольшим, при перемещении к середине В длины шпагата постепенно уменьшался, в точке В стал равным нулю, а затем начал по абсолютной величине увеличиваться, имея знак минус. Потенциал уменьшается вдоль внешней цепи от точки к точке в направлении тока.

   Рис. 73. Падение потенциала вдоль проводника с током

4. Свободные заряженные частицы, образующие ток, движутся непрерывным равномерным потоком и нигде не накапливаются и не исчезают. На это указывает постоянство тока в цепи.
5. Стационарное поле внутри проводника с постоянным током и магнитное поле вокруг него образуют электромагнитное поле.
6. При прохождении тока по проводнику поверхность последнего заряжена. В процессе прохождения тока заряды на поверхности проводника непрерывно обновляются.
7. Для поддержания электростатического поля энергию затрачивать не надо, а для поддержания стационарного электрического поля необходима непрерывная затрата энергии источника тока, так как энергия стационарного поля с помощью электрического тока превращается в другие виды энергии (механическую, внутреннюю).
8. Стационарное электрическое поле (как и электростатическое) — потенциальное.

От точки к точке проводника распространение электрического поля, а следовательно, и процесс направленного движения заряженных частиц, образующих ток, происходит со скоростью света, а направленное движение этих частиц происходит с очень малыми скоростями. Например, когда по медному проводу сечением 1 мм2 идет ток 1 а, электроны, образующие ток, движутся со скоростями порядка 0,07 мм/_сек.

Линии напряженности

Попытаемся теперь охарактеризовать электростатическое поле нескольких зарядов. В этом случае необходимо воспользоваться сложением векторных величин напряженностей всех зарядов. Внесем пробный заряд и запишем сумму векторов сил, действующих на этот заряд. Результирующее значение напряженности получится при разделении значений этих сил на величину пробного заряда. Данный метод называется принципом суперпозиции.

Напряженность электростатического поля принято изображать графически при помощи силовых линий, которые также называют линиями напряженности. Такое изображение можно получить, построив вектора напряженности поля в как можно большем количестве точек вблизи данного заряда или целой системы заряженных тел.

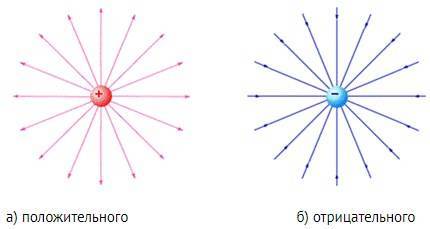
Рис. 4. Линии напряженности электрического поля точечного заряда (Источник)

Рассмотрим несколько примеров изображения силовых линий. Линии напряженности выходят из положительного заряда (рис. 4,а), то есть положительный заряд является источником силовых линий. Заканчиваются линии напряженности на отрицательном заряде (рис. 4,б).

Рассмотрим теперь систему, состоящую из положительного и отрицательного зарядов, находящихся на конечном расстоянии друг от друга (рис. 5). В этом случае линии напряженности направлены от положительного заряда к отрицательному.

Большой интерес представляет электрическое поле между двумя бесконечными плоскостями. Если одна из пластин заряжена положительно, а другая отрицательно, то в зазоре между плоскостями создается однородное электростатическое поле, линии напряженности которого оказываются параллельными друг другу (рис. 6). 

Рис. 5. Линии напряженности системы двух зарядов (Источник)  

Рис. 6. Линии напряженности поля между заряженными пластинами (Источник)

В случае неоднородного электрического поля величина напряженности определяется густотой силовых линий: там, где силовые линии гуще, величина напряженности поля больше (рис. 7).

Рис. 7. Неоднородное электрическое поле (Источник)

Определение: Линиями напряженности называют непрерывные линии, касательные к которым в каждой точке совпадают с векторами напряженности в этой точке.

Линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных и являются непрерывными.

Изображать электрическое поле с помощью силовых линий мы можем так, как сами посчитаем нужным, то есть число силовых линий, их густота ничем не ограничивается. Но при этом необходимо учитывать направление векторов напряженности поля и их абсолютные величины.

Очень важно следующее замечание. Как говорилось ранее, закон Кулона применим только для точечных покоящихся зарядов, а также заряженных шариков, сфер. Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает

Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает.

Список литературы

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2008.
2. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000.
3. Рымкевич А.П. Физика. Задачник. 10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.
4. Генденштейн Л.Э., Дик Ю.И. Физика. 10 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (базовый уровень) – М.: Мнемозина, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Nauka.guskoff.ru (Источник).
2. Youtube (Источник).
3. Physics.ru (Источник).

Домашнее задание

1. Стр. 378: № 1–3. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000. (Источник)
2. С каким ускорением движется электрон в поле напряженностью 10 кВ/м?
3. В вершинах равностороннего треугольника со стороной a находятся заряды +q, +q и –q. Найти напряженность поля Е в центре треугольника.

Вычисление напряженности и потенциала поля

Определение потенциала эквипотенциальной линии

Поскольку при моделировании
электростатических полей квазистационарным полем тока вопрос о полярности
электродов А и В является условным, будем полагать, что левый электрод А
имеет отрицательный потенциал, а правый В – положительный (рис. 4).

Найдем потенциал φ_i
для ί-й
эквипотенциальной линии. Положим потенциал отрицательного электрода равным
-0,5 U,
а потенциал положительного +0,5 U (U – напряжение,
подаваемое на электроды А и В потенциометра R).

Разность потенциалов между i-й линией и электродом
А имеет вид φ_i+1

φ_i — φ_A = φ_C – φ_А = I R_AC,

а между электродами А и В

φ_B – φ_A =
I R_AB =U.

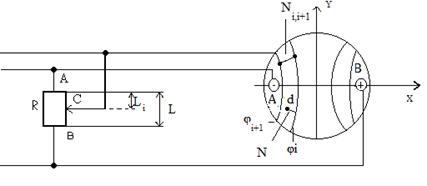
Рис. 4

Отсюда

. (11)

С другой стороны, сопротивление проводника
пропорционально его длине, т.е. R =
. С
учетом этого выражения соотношение (11) можно записать в виде

. (12)

Здесь l_i и
L –
длины участков АС и АВ в условных единицах соответственно. Учитывая (11),
(12) и φ_А = -0,5 U, получим

φ_i =
U (k_i
–0,5). (13)

Для данной установки равно U = 12 В.

Определение напряженности электростатического поля

Чтобы найти напряженность поля в точке N между i-й и i+1-й
эквипотенциальными линиями, воспользуемся формулой

Е
= – , (14)

где Е – среднее значение напряженности
между i-й и i+1-й
линиями в точке N
(рис. 4); U_i+1,_i = φ_i-φ_i+1 – разность потенциалов между i-й
и i+1-й
эквипотенциальными линиями; N_,i,i+1 – кратчайшее расстояние между этими
линиями.

Используя формулу (13), можно получить
выражение разности потенциалов

U_i+1,i =
, (15)

которое нужно поставить в (14). А значение
N_,i,i+1 измеряется на чертеже линейкой с учетом
выбранного масштаба.

Определение потенциала данной точки

Потенциал φ точки dполя,
расположенной между i-й

и i+1-й
эквипотенциальными линиями, находят из равенства

Е
= , (16)

Откуда

φ_d =
φ_i—
Е ·N.

Здесь Е определяется по формуле (14); N –
отрезок нормали, опущенной из точки d на i-ю линию, измеренный линейкой с учетом
выбранного масштаба.

Слайды и текст этой презентации

Слайд 1

Текст слайда:

Энергетическая характеристика электростатического поля

Работа электрического поля по перемещению электрического заряда. Потенциал электростатического поля.Разность потенциалов. Напряжение.Связь между разностью потенциалов и напряженностью поля.Эквипотенциальные поверхности.

900igr.net

Слайд 2

Текст слайда:

Wp – потенциальная энергия заряда в электростати-ческом поле

Работа электростатического поля по перемещению заряда

+q

d1

d2

1

2

-q

q

— работа поля равна изменению потенциальной энергии заряда, взятому с противоположным знаком

Слайд 3

Текст слайда:

Электрический заряд q перемещается по замкнутой траектории 1-2-3-4-1 как показано на рисунке в однородном электростатическом поле. Определите работу поля при данном перемещении заряда.

+q

1

2

-q

q

— работа поля не зависит от формы траектории и на замкнутой траектории равна нулю

3

4

Слайд 4

Текст слайда:

Энергетическая характеристика поля

Отношение потенциальной энергии Wp заряда q, помещенного в данную точку поля, к величине этого заряда не зависит от его значения, и, следовательно, является энергетической характеристикой электростатического поля, названной потенциалом:

Потенциал электростатического поля является величиной скалярной и определяет потенциальную энергию единичного положительного пробного заряда в данной точке поля.

Слайд 5

Текст слайда:

Разность потенциалов

Разность потенциалов между точками 1 и 2 равна отношению работы поля при перемещении заряда из точки 1 в точку 2 к величине этого заряда:

Разность потенциалов называют напряжением и обозначают U:

Если разность потенциалов равна 1 В, то при перемещении заряда в 1 Кл из одной точки в другую электрическое поле совершает работу 1 Дж.

Слайд 6

Текст слайда:

Связь между напряжением и напряженностью

Соотношение между напряженностью и напряжением:

Напряженность поля направлена в сторону убывания потенциала.

Слайд 7

Текст слайда:

Эквипотенциальные поверхности

Если работа поля при перемещении заряда равна нулю, то и разность потенциалов между начальной и конечной точками траектории тоже равна нулю. Это выполнится при перемещении заряда перпендикулярно линиям напряженности электрического поля.

Поверхность, все точки которой имеют равный потенциал, называется эквипотенциальной

Слайд 8

Текст слайда:

Напряженность и потенциал плоского конденсатора

Слайд 9

Текст слайда:

Напряженность и потенциал точечного заряда, сферы и плоскости

Слайд 10

Текст слайда:

Напряженность и потенциал поля, созданного при поляризации проводника в однородном поле

Описание

Электрическое поле положительного точечного электрического заряда, подвешенного на бесконечном листе проводящего материала. Поле изображается линиями электрического поля, линиями , которые повторяют направление электрического поля в пространстве.

Электрическое поле определяется в каждой точке пространства как сила (на единицу заряда), которая будет испытываться исчезающе малым положительным испытательным зарядом, если его удерживать в этой точке. Поскольку электрическое поле определяется в терминах силы , а сила является вектором (т. Е. Имеющим и величину, и направление ), из этого следует, что электрическое поле является векторным полем . Векторные поля такой формы иногда называют силовыми полями . Электрическое поле действует между двумя зарядами аналогично тому, как гравитационное поле действует между двумя массами , поскольку они оба подчиняются закону обратных квадратов с расстоянием. Это основа закона Кулона , который гласит, что для стационарных зарядов электрическое поле изменяется в зависимости от заряда источника и изменяется обратно пропорционально квадрату расстояния от источника. Это означает, что если бы заряд источника был удвоен, электрическое поле удвоилось бы, а если вы отодвинетесь вдвое дальше от источника, поле в этой точке будет только четверть его первоначальной силы.

Электрическое поле можно визуализировать с помощью набора линий , направление которых в каждой точке совпадает с направлением поля. Эта концепция была введена Майклом Фарадеем , чей термин « силовые линии » до сих пор иногда используется. Эта иллюстрация имеет то полезное свойство, что напряженность поля пропорциональна плотности линий. Силовые линии — это пути, по которым точечный положительный заряд будет следовать, когда он вынужден двигаться внутри поля, подобно траекториям, по которым массы следуют в гравитационном поле. Силовые линии из-за стационарных зарядов имеют несколько важных свойств, в том числе всегда исходят от положительных зарядов и заканчиваются отрицательными зарядами, они входят во все хорошие проводники под прямым углом, и они никогда не пересекаются и не замыкаются между собой. Линии поля представляют собой репрезентативную концепцию; поле фактически пронизывает все пространство между линиями. Может быть нарисовано больше или меньше линий в зависимости от точности, с которой желательно представить поле. Изучение электрических полей, создаваемых стационарными зарядами, называется электростатикой .

Закон Фарадея описывает взаимосвязь между изменяющимся во времени магнитным полем и электрическим полем. Один из способов сформулировать закон Фарадея состоит в том, что ротор электрического поля равен отрицательной производной по времени магнитного поля. В отсутствие изменяющегося во времени магнитного поля электрическое поле поэтому называется консервативным (то есть не завитым). Это означает, что существует два вида электрических полей: электростатические поля и поля, возникающие из изменяющихся во времени магнитных полей. В то время как отсутствие завитков статического электрического поля позволяет упростить лечение с использованием электростатики, изменяющиеся во времени магнитные поля обычно рассматриваются как компонент единого электромагнитного поля . Изучение изменяющихся во времени магнитных и электрических полей называется электродинамикой .

Сила порождаемая электрическими зарядами

Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.

Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.

Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы. Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля. В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.

Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях. Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля. Пробный заряд имеет некоторое количество заряда и обозначается символом q.

При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы — или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.

Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как

Стандартные метрические единицы измерения напряженности электрического поля возникают из его определения. Таким образом напряженность электрического поля определяется как сила равная 1 Ньютону (Н) деленному на 1 Кулон (Кл). Напряженность электрического поля измеряется в Ньютон/Кулон или иначе Н/Кл. В системе СИ также измеряется в Вольт/метр. Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.

В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).

Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет. Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q — скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза. Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз. Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.

Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.