Изучение электростатического поля

Сила порождаемая электрическими зарядами

Напряженность электрического поля является векторной величиной, а значит имеет численную величину и направление. Величина напряженности электрического поля имеет свою размерность, которая зависит от способа ее вычисления.

Электрическая сила взаимодействия зарядов описывается как бесконтактное действие, а иначе говоря имеет место дальнодействие, то есть действие на расстоянии. Для того, чтобы описать такое дальнодействие удобно ввести понятие электрического поля и с его помощью объяснить действие на расстоянии.

Давайте возьмем электрический заряд, который мы обозначим символом Q. Этот электрический заряд создает электрическое поле, то есть он является источником действия силы. Так как во вселенной всегда имеется хотя бы один положительный и хотя бы один отрицательный заряд, которые действую друг на друга на любом, даже бесконечно далеком расстоянии, то любой заряд является источником силы, а значит уместно описание создаваемого ими электрического поля. В нашем случае заряд Q является источником электрического поля и мы будем его рассматривать именно как источник поля.

Напряженность электрического поля источника заряда может быть измерена с помощью любого другого заряда, находящегося где-то в его окрестностях. Заряд, который используется для измерения напряженности электрического поля называют пробным зарядом, так как он используется для проверки напряженности поля. Пробный заряд имеет некоторое количество заряда и обозначается символом q.

При помещении пробного заряда в электрическое поле источника силы (заряд Q), пробный заряд будет испытывать действие электрической силы — или притяжения, или отталкивания. Силу можно обозначить как это обычно принять в физике символом F. Тогда величину электрического поля можно определить просто как отношение силы к величине пробного заряда.

Если напряженность электрического поля обозначается символом E, то уравнение может быть переписано в символической форме как

Стандартные метрические единицы измерения напряженности электрического поля возникают из его определения. Таким образом напряженность электрического поля определяется как сила равная 1 Ньютону (Н) деленному на 1 Кулон (Кл). Напряженность электрического поля измеряется в Ньютон/Кулон или иначе Н/Кл. В системе СИ также измеряется в Вольт/метр. Для понимания сути такого предмета как напряженность электрического поля гораздо важнее размерность в метрической системе в Н/Кл, потому как в такой размерность отражается происхождение такой характеристики как напряженность поля. Обозначение в Вольт/Метр делает понятие потенциала поля (Вольт) базовым, что в некоторых областях удобно, но не во всех.

В приведенном выше примере участвуют два заряда Q (источник) и q пробный. Оба этих заряда являются источником силы, но какой из них следует применять в вышеприведенной формуле? В формуле присутствует только один заряд и это пробный заряд q (не источник).

Напряженность электрического поля не зависит от количества пробного заряда q. На первый взгляд это может привести вас в замешательство, если, конечно, вы задумаетесь над этим. Беда в том, что не все имеют полезную привычку думать и пребывают в так называемом блаженном невежестве. Если вы не думаете, то и замешательства такого рода у вас и не возникнет. Так как же напряженность электрического поля не зависит от q, если q присутствует в уравнении? Отличный вопрос! Но если вы подумаете об этом немного, вы сможете ответить на этот вопрос. Увеличение количества пробного заряда q — скажем, в 2 раза — увеличится и знаменатель уравнения в 2 раза. Но в соответствии с Законом Кулона, увеличение заряда также увеличит пропорционально и порождаемую силу F. Увеличится заряд в 2 раза, тогда и сила F возрастет в то же количество раз. Так как знаменатель в уравнении увеличивается в два раза (или три, или четыре), то и числитель увеличится во столько же раз. Эти два изменения компенсируют друг друга, так что можно смело сказать, что напряженность электрического поля не зависит от количества пробного заряда.

Таким образом, независимо от того, какого количества пробный заряд q используется в уравнении, напряженность электрического поля E в любой заданной точке вокруг заряда Q (источника) будет одинаковой при измерении или вычислении.

Работа электростатического поля

Пусть имеется заряд, находящийся в электрическом поле. На него действует постоянная сила. Если носитель энергии перемещается из одной точки пространства в другую, то говорят о выполнении им работы. В простейшем случае можно рассмотреть однородное поле. В качестве него можно использовать конденсатор. В нём правая пластина пусть будет заряжена положительно, а левая — отрицательно.

Считается, что линии электрического поля будут направлены от плюса к минусу. В некоторой точке этого однородного состояния находится заряд. Для конкретики его можно принять положительным и обозначить буквой A. Под действием сил он перемещается в точку Б. Задача состоит в нахождении работы, совершаемой полем для изменения положения заряженной частицы.

Из механики известно, что такое действие может быть определенно произведением действующей на заряд силы и модуля перемещения, умноженным на косинус угла между ними: A = F * S * cos (a). Так как заряд положительный, то его направление будет совпадать с линиями электрического поля (напряжённостью E). Сила находится по формуле: F = q * E. Тогда, подставляя модуль этого вектора в выражение для работы, можно записать: A = q * E * S * cos (a).

Произведение S * cos (a) представляет собой проекцию отрезка перемещения на направление электрического поля. Изобразить её можно как перпендикуляр, опущенный на E. В результате получится прямоугольный треугольник. Обозначить прилежащий катет (проекцию) можно буквой d. В итоге формула для работы примет вид: A = q * E * d, где:

• q — заряд;
• E — напряжённость;
• d — проекция перемещения.

Таким свойством обладают силы тяжести и упругости. Называются они потенциальными. Следовательно, работа по перемещению электричества является такой же. Происходит она за счёт потенциальной энергии заряда, находящего в поле. Поэтому работа равняется уменьшению её значения. Выполненное действие пропорционально заряду, то есть отношению: W / q. Эта величина и получила название «электрический потенциал».

§ 54. Электрическое поле внутри проводника с током

В проводниках тока имеется большое количество хаотически движущихся свободных заряженных частиц — электронов, ионов. Если эти частицы заставить помимо хаотического движения еще двигаться в целом в виде направленного потока, то получится электрический ток. В электрических цепях частицы, образующие тек, приводятся в направленное движение электрическим полем, которое создает источник тока в проводах цепи вследствие наличия на его полюсах разности потенциалов. Электрическое поле внутри и вокруг неподвижного проводника с постоянным током называется стационарным электрическим полем.

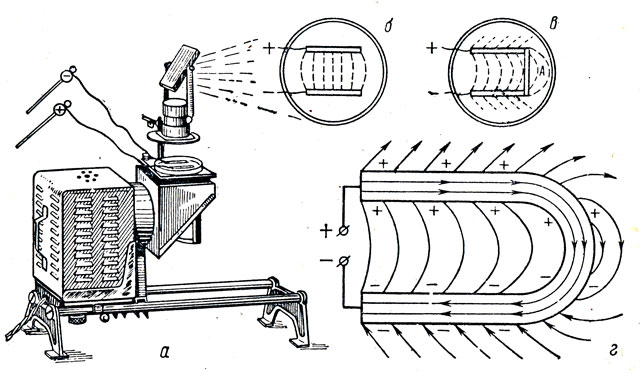Рис. 72. Линии напряженности стационарного электрического поля

Наблюдать такое поле можно на следующем опыте. В проекционной ванночке имеется тонкий слой прозрачного жидкого диэлектрика, в котором находятся мелко нарезанные волоски и две параллельные влажные палочки (рис. 72, а). Присоединим проводники (палочки) к источнику напряжения (к шарикам электрофорной машины). Волоски приходят в движение и располагаются, создавая картину электростатического поля заряженных проводников, в котором линии напряженности нормальны к поверхности проводников (рис. 72, б). Замкнем цепь в ванночке деревянной палочкой А (рис. 72, в). В проводнике и вокруг него образуется стационарное электрическое поле. Под его действием возникает ток, и вид прежнего поля изменяется. Сравнивая картину электростатического и стационарного полей, видим, что* между ними есть отличие:

1. Линии напряженности электростатического поля заряженного проводника перпендикулярны к поверхности проводника, а стационарного поля вне проводника — наклонны в направлении тока (рис. 72, г). Обнаружить стационарное электрическое поле вне проводника такими приемами, как обнаруживается электростатическое поле зарядов гильзой, нельзя из-за малой напряженности первого. Внутри прямолинейного проводника стационарное поле однородное (его линии напряженности направлены вдоль проводника), внутри криволинейного — неоднородное.
2. В любой точке стационарного поля есть напряженность, на что указывает наличие тока в цепи.

3. Потенциал поля внутри проводника и на его поверхности уменьшается в направлении движения тока. В этом можно убедиться на таком опыте (рис. 73). Приведя в действие электрофорную машину, получим в цепи из шпагата (потертого влажной тряпочкой) электрический ток. Начнем электрометр, соприкасающийся стержнем, со шпагатом, передвигать вдоль цепи. Видим, что потенциал в разных точках цепи различен. У шарика А он был наибольшим, при перемещении к середине В длины шпагата постепенно уменьшался, в точке В стал равным нулю, а затем начал по абсолютной величине увеличиваться, имея знак минус. Потенциал уменьшается вдоль внешней цепи от точки к точке в направлении тока.

   Рис. 73. Падение потенциала вдоль проводника с током

4. Свободные заряженные частицы, образующие ток, движутся непрерывным равномерным потоком и нигде не накапливаются и не исчезают. На это указывает постоянство тока в цепи.
5. Стационарное поле внутри проводника с постоянным током и магнитное поле вокруг него образуют электромагнитное поле.
6. При прохождении тока по проводнику поверхность последнего заряжена. В процессе прохождения тока заряды на поверхности проводника непрерывно обновляются.
7. Для поддержания электростатического поля энергию затрачивать не надо, а для поддержания стационарного электрического поля необходима непрерывная затрата энергии источника тока, так как энергия стационарного поля с помощью электрического тока превращается в другие виды энергии (механическую, внутреннюю).
8. Стационарное электрическое поле (как и электростатическое) — потенциальное.

От точки к точке проводника распространение электрического поля, а следовательно, и процесс направленного движения заряженных частиц, образующих ток, происходит со скоростью света, а направленное движение этих частиц происходит с очень малыми скоростями. Например, когда по медному проводу сечением 1 мм2 идет ток 1 а, электроны, образующие ток, движутся со скоростями порядка 0,07 мм/_сек.

Общая характеристика

Электрическим полем называется специфическая разновидность материи, формируемая микротелами, имеющими заряды. Тем не менее, это не только совокупность заряженных тел: данным термином именуется также микрополе, которое формирует в пространстве каждое заряженное тело. Именно совокупность этих микрополей и создаёт электрические поля в привычном для нас понимании.

Существование и непрерывное функционирование электрического поля обусловлено непрерывным взаимодействием частиц, имеющих заряды, в ходе которого они непосредственно сообщают электромагнитную энергию один другому посредством электрических полей, которые окружают каждое из них. Графически электрическое поле следует изображать в виде схематичной совокупности линий, в физической науке именуемых силовыми.

Силовые линии

Благодаря достижениям современной физики мы знаем, что электрические силы объясняют все химические и физические свойства веществ, от атома до животной клетки. Естествоиспытателями, которые заложили фундамент научного знания об электрическом поле, были Андре-Мари Ампер, Майкл Фарадей и Джеймс Клерк Максвелл.

Линии напряженности

Попытаемся теперь охарактеризовать электростатическое поле нескольких зарядов. В этом случае необходимо воспользоваться сложением векторных величин напряженностей всех зарядов. Внесем пробный заряд и запишем сумму векторов сил, действующих на этот заряд. Результирующее значение напряженности получится при разделении значений этих сил на величину пробного заряда. Данный метод называется принципом суперпозиции.

Напряженность электростатического поля принято изображать графически при помощи силовых линий, которые также называют линиями напряженности. Такое изображение можно получить, построив вектора напряженности поля в как можно большем количестве точек вблизи данного заряда или целой системы заряженных тел.

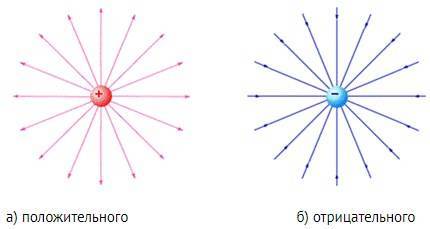
Рис. 4. Линии напряженности электрического поля точечного заряда (Источник)

Рассмотрим несколько примеров изображения силовых линий. Линии напряженности выходят из положительного заряда (рис. 4,а), то есть положительный заряд является источником силовых линий. Заканчиваются линии напряженности на отрицательном заряде (рис. 4,б).

Рассмотрим теперь систему, состоящую из положительного и отрицательного зарядов, находящихся на конечном расстоянии друг от друга (рис. 5). В этом случае линии напряженности направлены от положительного заряда к отрицательному.

Большой интерес представляет электрическое поле между двумя бесконечными плоскостями. Если одна из пластин заряжена положительно, а другая отрицательно, то в зазоре между плоскостями создается однородное электростатическое поле, линии напряженности которого оказываются параллельными друг другу (рис. 6). 

Рис. 5. Линии напряженности системы двух зарядов (Источник)  

Рис. 6. Линии напряженности поля между заряженными пластинами (Источник)

В случае неоднородного электрического поля величина напряженности определяется густотой силовых линий: там, где силовые линии гуще, величина напряженности поля больше (рис. 7).

Рис. 7. Неоднородное электрическое поле (Источник)

Определение: Линиями напряженности называют непрерывные линии, касательные к которым в каждой точке совпадают с векторами напряженности в этой точке.

Линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных и являются непрерывными.

Изображать электрическое поле с помощью силовых линий мы можем так, как сами посчитаем нужным, то есть число силовых линий, их густота ничем не ограничивается. Но при этом необходимо учитывать направление векторов напряженности поля и их абсолютные величины.

Очень важно следующее замечание. Как говорилось ранее, закон Кулона применим только для точечных покоящихся зарядов, а также заряженных шариков, сфер. Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает

Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает.

Список литературы

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: учеб. для 10 кл. общеобразоват. учреждений: базовый и профил. уровни. – М.: Просвещение, 2008.
2. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000.
3. Рымкевич А.П. Физика. Задачник. 10-11 кл.: пособие для общеобразоват. учреждений. – М.: Дрофа, 2013.
4. Генденштейн Л.Э., Дик Ю.И. Физика. 10 класс. В 2 ч. Ч. 1. Учебник для общеобразовательных учреждений (базовый уровень) – М.: Мнемозина, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Nauka.guskoff.ru (Источник).
2. Youtube (Источник).
3. Physics.ru (Источник).

Домашнее задание

1. Стр. 378: № 1–3. Касьянов В.А. Физика. 10 кл.: учеб. для общеобразоват. учеб. заведений. — М.: Дрофа, 2000. (Источник)
2. С каким ускорением движется электрон в поле напряженностью 10 кВ/м?
3. В вершинах равностороннего треугольника со стороной a находятся заряды +q, +q и –q. Найти напряженность поля Е в центре треугольника.

Закон Кулона

В 1785 г. французский физик Шарль Кулон экспериментально установил основной закон электростатики – закон взаимодействия двух неподвижных точечных заряженных тел или частиц.

Закон взаимодействия неподвижных электрических зарядов – закон Кулона – основной (фундаментальный) физический закон и может быть установлен только опытным путем. Ни из каких других законов природы он не вытекает.

Если обозначить модули зарядов через |q₁| и |q₂|, то закон Кулона можно записать в следующей форме:

\(~F = k \cdot \frac{|q_1| \cdot |q_2|}{r^2}\) , (1)

где k – коэффициент пропорциональности, значение которого зависит от выбора единиц электрического заряда. В системе СИ \(~k = \frac{1}{4 \pi \cdot \varepsilon_0} = 9 \cdot 10^9\) Н·м2/Кл2, где ε – электрическая постоянная, равная 8,85·10-12 Кл2/Н·м2 .

Формулировка закона:

сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

Эту силу называют кулоновской.

Закон Кулона в данной формулировке справедлив только для точечных заряженных тел, т.к. только них понятие расстояния между зарядами имеет определенный смысл. Точечных заряженных тел в природе нет. Но если расстояние между телами во много раз больше их размеров, то ни форма, ни размеры заряженных тел существенно, как показывает опыт, не влияют на взаимодействие между ними. В этом случае тела можно рассматривать как точечные.

Легко обнаружить, что два заряженных шарика, подвешенные на нитях, либо притягиваются друг к другу, либо отталкиваются. Отсюда следует, что силы взаимодействия двух неподвижных точечных заряженных тел направлены вдоль прямой, соединяющей эти тела. Подобные силы называют центральными. Если через \(~\vec F_{1,2}\) обозначить силу действующую на первый заряд со стороны второго, а через \(~\vec F_{2,1}\) – силу, действующую на второй заряд со стороны первого (рис. 1), то, согласно третьему закону Ньютона, \(~\vec F_{1,2} = -\vec F_{2,1}\) . Обозначим через \vec r_{1,2} радиус-вектор, проведенный от второго заряда к первому (рис. 2), тогда

\(~\vec F_{1,2} = k \cdot \frac{q_1 \cdot q_2}{r^3_{1,2}} \cdot \vec r_{1,2}\) . (2)

Если знаки зарядов q₁ и q₂ одинаковы, то направление силы \(~\vec F_{1,2}\) совпадает с направлением вектора \(~\vec r_{1,2}\) ; в противном случае векторы \(~\vec F_{1,2}\) и \(~\vec r_{1,2}\) направлены в противоположные стороны.

Зная закон взаимодействия точечных заряженных тел, можно вычислить силу взаимодействия любых заряженных тел. Для этого тела нужно мысленно разбить на такие малые элементы, чтобы каждый из них можно было считать точечным. Складывая геометрически силы взаимодействия всех этих элементов друг с другом, можно вычислить результирующую силу взаимодействия.

Открытие закона Кулона – первый конкретный шаг в изучении свойств электрического заряда. Наличие электрического заряда у тел или элементарных частиц означает, что они взаимодействуют друг с другом по закону Кулона. Никаких отклонений от строгого выполнения закона Кулона в настоящее время не обнаружено.

Возникновение, генерация, приложения статических зарядов

Встречается в природе и в повседневной жизни:

• Грозовые облака
• Электростатическое поле земли
• Электростатический разряд , например Б. после зарядки: ходьба по ковровому покрытию, пластиковые перила, сидение на креслах с чехлами из синтетического волокна , расчесывание пластиковой расческой, снятие свитера из синтетического волокна.

Генерация высоких напряжений путем переноса статических зарядов (в исследованиях, обучении, промышленности):

• Электрификационная машина
• Ленточный генератор
• Машина влияния

Приложения:

• Электростатический фильтр
• электростатическая окраска распылением
• Фиксация листов бумаги на планшетных плоттерах и
• Порошковое покрытие
• ксерография

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ​\( C \)​, единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

Формула для вычисления электроемкости:

где ​\( q \)​ – заряд проводника, ​\( \varphi \)​ – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

где ​\( q \)​ – модуль заряда одной из обкладок,
​\( U \)​ – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ​\( S \)​, находящиеся на расстоянии ​\( d \)​ друг от друга.

Электроемкость плоского конденсатора:

где ​\( \varepsilon \)​ – диэлектрическая проницаемость вещества между обкладками,\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

Виды конденсаторов:

• по типу диэлектрика – воздушный, бумажный и т. д.;
• по форме – плоский, цилиндрический, сферический;
• по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

Общая емкость:

Последовательное соединение конденсаторов

При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

Общее напряжение:

Величина, обратная общей емкости:

При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Напряженность электрического поля

Какое поле называют электростатическим?

Электростатическое поле – это электрическое поле, которое окружает неподвижные и не меняющиеся со временем заряды.

Очень часто в контексте темы электростатическое поле будет именоваться электрическим для краткости.

Электрическое поле может быть создано сразу несколькими заряженными телами. Такое поле также можно исследовать с помощью пробного заряда. В этом случае мы будем оценивать результирующую силу, которая будет равна геометрической сумме сил каждого из заряженных тем в отдельности.

Напряженность электрического поля, которая создается в определенной точке пространства системой зарядов, будет равна векторной сумме напряженностей электрических полей:

Электрическое поле подчиняется принципу суперпозиции.

Согласно формуле, напряженность электростатического поля, которое создается точечным зарядом Q на расстоянии r от него, в соответствии с законом Кулона, будет равна по модулю:

E = 1 4 πε 0 · Q r 2 .

Это поле называется кулоновским.

В кулоновском поле направление вектора E ⇀ зависит от знака заряда Q : если Q > 0 , то вектор E ⇀ направлен по радиусу от заряда, если Q 0 , то вектор E ⇀ направлен к заряду.

Обратимся к иллюстрации. На рисунке для большей наглядности мы используем силовые линии электрического поля. Они проходят таким образом, чтобы направление вектора E ⇀ в каждой из точек пространства совпадало с направлением касательной к силовой линии. Густота силовых линий соответствует модулю вектора напряженности поля.

Рисунок 1 . 2 . 1 . Силовые линии электрического поля.

Мы можем использовать как положительные, так и отрицательные точечные заряды. Оба эти случая мы изобразили на рисунке. Электростатическое поле, которое создается системой зарядов, мы можем представить как суперпозицию кулоновских полей точечных зарядов. В связи с этим мы можем рассматривать поля точечных зарядов как элементарные структурные единицы любого электрического поля.

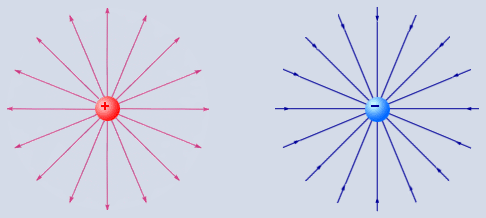
Рисунок 1 . 2 . 2 . Силовые линии кулоновских полей.

Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r → от заряда Q к точке наблюдения. Тогда при Q > 0 вектор E → параллелен r → , а при Q 0 вектор E → антипараллелен r → .

Следовательно можно записать:

E → = 1 4 π ε 0 · Q r 3 r → ,

где r – модуль радиус-вектора r → .

По заданному распределению зарядов можно определить электрическое поле E → . Такие задачи часто встречаются в таком разделе физики как электростатика. Рассмотрим пример такой задачи.

Предположим, что нам нужно найти электрическое поле длинной однородно заряженной нити на расстоянии R от нее. Для большей наглядности мы привели схему на рисунке ниже.

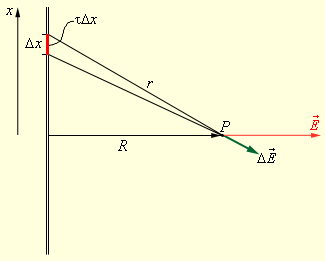
Рисунок 1 . 2 . 3 . Электрическое поле заряженной нити.

Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δ x нити, с зарядом τ Δ x , где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей ∆ E → . Результирующее поле оказывается равным

Вектор E → везде направлен по радиусу R → . Это следует из симметрии задачи.

Даже в таком простом примере вычисления могут быть достаточно громоздкими. Упростить математические расчеты позволяет теорема Гаусса, которая выражает фундаментальное свойство электрического поля.

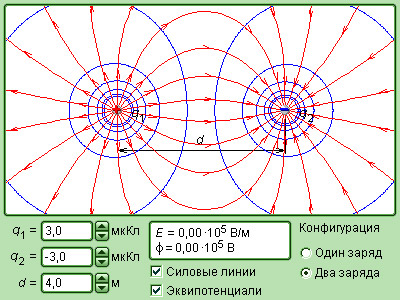
Рисунок 1 . 2 . 4 . Модель электрического поля точечных зарядов.

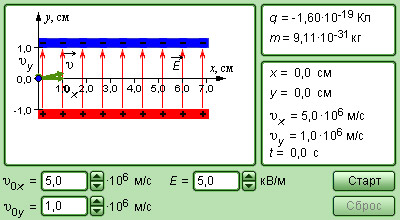
Рисунок 1 . 2 . 5 . Модель движения заряда в электрическом поле.

Условия равновесного состояния заряда в проводнике

Можно представить пару точечных зарядов, модули которых одинаковы, а знаки противоположны. Такие заряженные частицы +q и –q отдалены друг от друга на некоторое расстояние. Они создают электростатическое поле, в котором наблюдают системы с взаимно перпендикулярными силовыми линиями и эквипотенциальными поверхностями. В качестве одной из таких поверхностей представлена плоскость. Она пролегает сквозь середину отрезка, который соединяет заряженные частицы. Плоскость обладает нулевым потенциалом, так как, исходя из принципа суперпозиции, если точки удалены на равные расстояния r1 = r2 от заряженных частиц, то:

\(\varphi =\varphi _{1}+\varphi _{2}=k\frac{q}{r_{1}}-k\frac{q}{r_{2}}=0\)

Далее необходимо совместить плоскость и тонкую проводящую пластину с последующим ее заземлением.

Можно наблюдать, что поле при этом сохранит стабильность, так как все точки пластины обладают одинаковым потенциалом, равным нулю. При исключении заряда –q, который наблюдается за проводящей пластиной, поле перед ней не изменится. Исходя из этого, можно сделать вывод о том, что при приближении тонкой проводящей заземленной пластины к точечному заряду электрическое поле, которое создают реальный заряд и его мнимое изображение противоположного знака в пластине, будет совпадать с полем в зеркале. Способ электростатических изображений не является универсальным методом, однако с его помощью можно упростить решение многих задач.

Графическое изображение электрических полей

Чтобы задать электрическое поле, надо указать направление и значение силы, действующей на пробный заряд, когда его разместить в той или иной точке поля. Это можно сделать графическим способом, предложенным Фарадеем, с помощью силовых линий (линий напряженности электрического поля).

Направление силовых линий совпадает с направлением вектора напряженности. В случае точечных зарядов силовые линии направлены от положительного заряда и заканчиваются в бесконечности или начинаются в бесконечности и идут к отрицательного заряда.

Сложнее провести линии напряженности, когда поле создано несколькими зарядами, например двумя. Такая система из двух зарядов называется диполем. Провести линию так, чтобы векторы напряженности в каждой точке совпадали с ней, преимущественно нельзя. Поэтому линии напряженности проводят так, чтобы векторы напряженности были направлены по касательной

Линии напряженности точечных зарядов (а, б), диполя (в)

Линии напряженности (силовые линии) электрического поля — непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с вектором напряженности поля.

На рисунке изображена еще несколько примеров электрических полей.

Графическое изображение электрических полей: а — одинаковых по значению разноименных зарядов; б — одинаковых по значению одноименных зарядов; в — двух пластин, заряженных разноименными зарядами одинаковой величины.

Изображая электрическое поле графически, нужно помнить, что линии напряженности нигде не пересекаются друг с другом, не должны прерываться между зарядами, начинаются на положительном заряде (или в бесконечности) и заканчиваются на отрицательном заряде (или в бесконечности).

Поле, напряженность которого во всех точках одинакова по модулю и направлению, называют однородным электростатическим полем. Примером такого поля является поле внутри пространства между заряженными пластинами (у краев пластин поле неоднородно).

§ 19. Напряжённость электростатического поля. Принцип суперпозиции

Для изучения свойств электростатического поля удобно использовать такую его характеристику, которая не зависит от числового значения пробного заряда и позволяет определить силу, действующую на заряд со стороны поля в любой его точке. Для гравитационного поля такой характеристикой, не зависящей от массы тела, является ускорение свободного падения . Какая физическая величина является характеристикой электростатического поля?

Напряжённость электростатического поля. Пусть электростатическое поле создано в вакууме точечным зарядом Q > 0. Если в некоторую точку поля поместить пробный положительный заряд q, на него будет действовать кулоновская сила отталкивания, модуль которой .

Сила не может служить характеристикой поля, так как её модуль пропорционален значению пробного заряда q. Однако отношение модуля силы, которой электростатическое поле точечного заряда Q действует на пробный заряд q, не зависит от значения пробного заряда:

(19.1)

и, следовательно, может служить характеристикой поля.

Эту характеристику называют напряжённостью электростатического поля и обозначают . Напряжённость характеризует силовое действие поля на вносимые в него заряды.

Напряжённость электростатического поля — физическая векторная величина, равная отношению силы, которой поле действует на пробный заряд, к значению этого заряда:

(19.2)

С учётом выражений (19.1) и (19.2) можно определить модуль напряжённости электростатического поля, созданного точечным зарядом Q, в точке, находящейся на расстоянии r от него:

Таким образом, модуль напряжённости поля, создаваемого в вакууме точечным зарядом, прямо пропорционален модулю этого заряда и обратно пропорционален квадрату расстояния между зарядом и точкой, в которой определяют значение напряжённости.

Если заряд Q находится в однородной среде с диэлектрической проницаемостью ε, то модуль напряжённости поля .

Из выражения  следует, что единицей напряжённости электростатического поля в СИ является ньютон на кулон . В СИ широко используют другое название этой единицы — вольт на метр .

Зная напряжённость электростатического поля, можно определить силу, действующую на любой точечный заряд в любой точке этого поля:

(19.3)

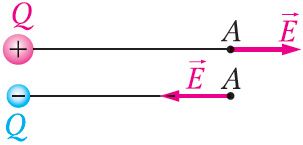Рис. 104

Напряжённость поля, как и сила, величина векторная. Направление напряжённости поля совпадает с направлением силы, действующей на положительный пробный электрический заряд. Напряжённость в любой точке электростатического поля точечного заряда направлена вдоль прямой, соединяющей эту точку и точечный заряд, создающий поле. Напряжённость поля, созданного точечным положительным зарядом Q > 0, направлена от заряда, а напряжённость поля, созданного точечным отрицательным зарядом Q < 0, — к заряду (рис. 104).

От теории к практике

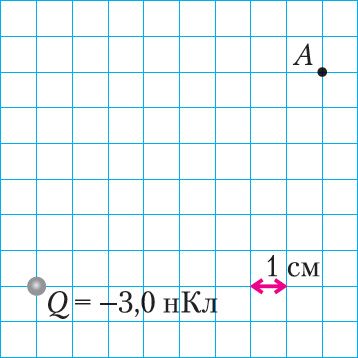Рис. 105

1. Как изменится модуль напряжённости в некоторой точке поля, созданного точечным зарядом Q, если: а) расстояние r от заряда до этой точки увеличить вдвое; б) заряд Q увеличить вдвое, а расстояние r от заряда до этой точки уменьшить вдвое?

2. Как направлена в точке А напряжённость поля, созданного неподвижным точечным зарядом (рис. 105)? Чему равен модуль напряжённости поля в этой точке?

Рис. 105.1

Модуль напряжённости поля уединённой проводящей сферы радиусом R, заряд которой Q (рис. 105.1), в точках на её поверхности r = R и вне сферы на расстоянии r > R от её центра определяют по формуле . В точках, находящихся внутри проводящей сферы r < R, напряжённость равна нулю , если внутри этой сферы нет электрических зарядов.

Напряжённость электростатического поля, создаваемого равномерно заряженной бесконечной плоскостью, одинакова во всех точках полупространства с каждой стороны от плоскости (при этом ), а её модуль

где S — площадь некоторого участка плоскости, — модуль заряда этого участка (рис. 105.2).

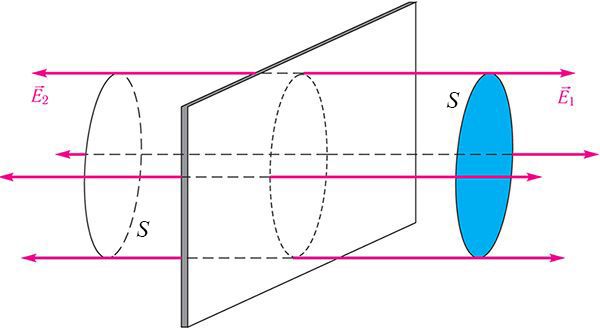Рис. 105.2

Интересно знать

Кроме гравитационного поля у Земли есть электрическое и магнитное поля. Модуль напряжённости электрического поля у поверхности Земли в среднем составляет . Электрическое поле Земли меняется во времени. Избыточный отрицательный электрический заряд земного шара колеблется около –6 · 105 Кл.