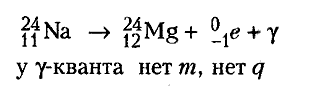Физика. 11 класс

Соотношение N: Z и магические числа

Итак, отношение нейтрона к протону или Соотношение N: Z является основным фактором, определяющим, является ли атомное ядро ​​стабильным. Более легкие элементы (Z <20) предпочитают иметь одинаковое количество протонов и нейтронов или N: Z = 1. Более тяжелые элементы (Z = 20–83) предпочитают отношение N: Z, равное 1,5, поскольку для изоляции от нейтронов требуется больше нейтронов. сила отталкивания между протонами.

Есть также то, что называется магические числа, которые являются числами нуклонов (или протонов или нейтронов), которые являются особенно стабильными. Если оба числа протонов и нейтронов являются этими значениями, ситуация называется двойные магические числа, Вы можете думать об этом как о ядре, эквивалентном правилу октета, управляющему стабильностью электронной оболочки. Магические числа немного отличаются для протонов и нейтронов:

• протон: 2, 8, 20, 28, 50, 82, 114
• нейтроны: 2, 8, 20, 28, 50, 82, 126, 184

Для дальнейшего усложнения стабильности существуют более стабильные изотопы с четно-четным Z: N (162 изотопа), чем четное: нечетное (53 изотопа), чем нечетное: четное (50), чем нечетное: нечетное (4).

Радиоактивность — что это за явление

Понятие «радиоактивность» было введено Марией Склодовской-Кюри. Оно тождественно понятию радиоактивный распад.

В определении присутствует термин изотоп. Прежде чем рассмотреть его, вспомним определение нуклида. 

Для обозначения определенного нуклида используют запись вида 

X ZA, 

где X — символ химического элемента, A — массовое (нуклонное) число, Z — зарядовое (протонное) число.

Количество нейтронов в ядре N=A−Z 

Это значит, что в изотопах одинаковое число протонов, но разное число нейтронов. 

Всего известно более двух тысяч радиоактивных изотопов. Для сравнения, стабильных открыто около 280.

Ученые разделяют нуклиды на стабильные и нестабильные. Нестабильные, также известные как радионуклиды, со временем распадаются. Стабильные же способны существовать в неизменном виде неопределенно долгий промежуток времени.

Суть явления радиоактивности заключается в том, что при распаде ядра нестабильного атома из него с большой скоростью вылетает целое число частиц с высокой энергией. Вещества, которые содержат радиоактивные ядра, называют радиоактивными. 

В современной химии выделяют естественную и искусственную радиоактивность. 

Примером естественной радиоактивности служит солнечная радиация. В ядре солнца постоянно происходят термоядерные реакции, в ходе которых водород превращается в гелий. 

Техногенная радиоактивность применяется людьми. Например, на атомных электростанциях электрическую энергию получают за счет искусственно созданных ядерных реакций.

В результате экспериментов было установлено, что в периодической системе Менделеева радиоактивны все элементы, начиная с висмута. Их порядковый номер больше 82.

Единицы измерения

В химии существует несколько единиц измерения радиоактивности:

• беккерель;
• кюри;
• резерфорд.

В Международной системе единиц (СИ) единицей измерения активности радионуклида является беккерель. На русском языке он обозначается как Бк, в международном формате — Bq. 

Эту единицу назвали в честь Антуана Беккереля, одного из первооткрывателей радиоактивности. Один Беккерель равен одному распаду в секунду.

Бк=с-1

В Международной СИ секунде в минус первой степени равен не только беккерель, но и герц

Важно не путать их: беккерель используют для измерения случайных процессов распада, а герц — для периодических процессов. Их природа различна

Один Беккерель — это маленькая единица измерения, так что на практике принято использовать кратные единицы.

Внесистемная, но широко распространенная единица — кюри. Ее используют для измерения активности радионуклидов. На русском обозначается как Ки, в международных исследованиях — Ci. Названа она в честь Пьера Кюри и Марии Склодовской-Кюри.

Точно установлена связь между значениями Ки и Бк:

1 Ки = 3,7⋅1010 Бк

Перевести значения из Бк в Ки сложнее, т.к. соотношение приблизительно:

1 Бк ≈ 2,7027⋅10-11 Ки

Еще одна единица измерения, которой в современности пользуются редко — резерфорд. Его обозначают как Рд или Rd в русском и международном стандартах соответственно. Единица тоже названа в честь ученого — Эрнеста Резерфорда, также изучавшего природу радиоактивности.

Один резерфорд равен 10^6 распадам в 1 секунду. Точно равенство:

1 Рд = 1⋅106 Бк = 1 МБк 

В дозиметрии используют свои единицы облучения:

• грэй;
• зиверт;
• бэр.

Поглощенную дозу в Международной СИ измеряют в единицах грэй (Гр). Один грэй равен энергии излучения в 1 Дж, поглощенной 1 кг вещества.

Эквивалентную дозу, т.е. произведение поглощенной дозы на коэффициент качества излучения, в Си измеряют в зивертах. Один зиверт эквивалентен излучению, создающему такой же биологический эффект, как и поглощенная доза в 1 Гр гамма-излучения или рентгеновского излучения.

1 Зв = 1 Джкг

Внесистемная единица измерения эквивалентной дозы — бэр. Бэр расшифровывается как «биологический эквивалент рентгена». 

За один бэр принято считать такое количество энергии излучения, поглощенного 1 кг вещества, при котором биологическое воздействие соответствует поглощенной дозе в 1 рад гамма-излучения или рентгеновского излучения. То есть:

1 бэр=,01 Зв=100 эргг

Для измерения воздействия радиации используют также понятие мощность дозы. Это доза, полученная объектом за выбранную единицу времени.

Физическая природа радиоактивности и виды радиоактивных излучений

Изучением радиоактивного излучения также занимался английский физик Эрнест Резерфорд. Он первый поставил эксперимент, который позволил обнаружить сложный состав этого излучения. Ученый собрал установку, изображенную на рисунке ниже.

Резерфорд поместил препарат радия на дно узкого канала в куске свинца. Напротив открытого конца канала он расположил фоточувствительную пластинку. В результате излучение от радия исходила из канала и попадало на эту пластинку. Но ученый расположил магнит так, что излучающимся частицам приходилось проходить сквозь созданное им магнитное поле. Для чистоты эксперимента вся установка помещалась в сосуд с откачанным воздухом (в вакуум).

Если магнит убрать, то на фотопластинке обнаруживалось лишь одно темное пятно напротив канала. Но если вернуть магнит на место, то пучок распадается на 3 части. Причем одна часть первичного потока сохранила свое направление (пятно получилось напротив пластинки), а две другие его составляющие отклонялись в противоположные стороны.

Как это можно объяснить? Известно, что в магнитом поле меняют свое направление движения только заряженные частицы. Следовательно, опыт продемонстрировал наличие электрических зарядом у двух пучков (у одного из них заряд оказался нейтральным, так как направление изменено не было). Узнать знак этих пучков можно, применив правило левой руки. Так, один из них оказался положительно заряженным, а второй — отрицательно заряженным.

Дальнейшие исследования радиоактивного излучения позволили выяснить природу этих видов излучения. Их разделили на 3 вида и дали им следующие названия:

• Альфа-излучение — поток положительно заряженных α-частиц. Они представляют собой полностью ионизированные атомы гелия (ядра гелия), летящие со скоростью 14–20 тыс. км/с.
• Бета-излучение — поток отрицательно заряженных β-частиц, или электронов. Они летят со скоростью, приближенной к скорости света (около 0,999c).
• Гамма-излучение — электромагнитное излучение с длиной волны менее 10-10 м, имеющее ярко выраженные корпускулярные свойства, то есть являющееся потоком γ-квантов.

В чем же заключается физическая сущность явления радиоактивности? Чтобы ответить на вопрос, нужно провести исследование самого радиоактивного вещества.

Опыты по изучению радиоактивности, проводимые Резерфордом вместе с английским ученым Ф. Содди, дали понять, что во время радиоактивного излучения исходный химический элемент превращается в другое химический элемент. Такое превращение ученые назвали радиоактивным распадом.

Радиоактивный распад — превращение радиоактивного вещества в другой химический элемент, сопровождающееся радиоактивным излучением.

Радиоактивность — самопроизвольное превращение ядер одних химических элементов в ядра других химических элементов, сопровождаемое испусканием различных частиц или ядер.

Виды распадов:

α-распад. Ядро теряет одну α-частицу, в результате чего оно теряет массу, равную 4 атомным единицам массы (а.е.м.). При этом из исходного вещества образуется новый химический элемент, смещенный на 2 клетки к началу периодической системы Менделеева.

Символически α-распад можно записать так:

M.ZX→M−4.Z−2Y+42He

M.ZX — распадающееся радиоактивное вещество с массовым числом M и зарядовым числом Z, M−4.Z−2Y — новый химический элемент с массовым числом (M–4) и зарядовым числом (Z–2), 42He — излучаемая α-частица.

β-распад. Ядро теряет одну β-частицу (электрон), в результате чего он меняет заряд на 1 единицу, а его масса почти не изменяется. При этом из исходного вещества образуется новый химический элемент, смещенный на 1 клетку к концу периодической системы Менделеева.

Символически β -распад можно записать так:

M.ZX→.MZ+1Y+−1e

M.ZX — распадающееся радиоактивное вещество с массовым числом M и зарядовым числом Z, .MZ+1Y — новый химический элемент с массовым числом M и зарядовым числом (Z+1), −1e — излучаемый электрон.

Внимание! Фактически при β-распаде один нейтрон превращается в протон с испусканием электрона. γ-распад

Ядро теряет одну γ-частицу. В результате не образуется нового вещества, и масса ядра практически не изменяется

γ-распад. Ядро теряет одну γ-частицу. В результате не образуется нового вещества, и масса ядра практически не изменяется.

Пример №1. Записать правило α-распада вещества 238.92U.

Для записи формулы используем формулу:

M.ZX→M−4.Z−2Y+42He

Зарядовое число уменьшится на 2: 92–2 = 90. Этому порядковому номеру соответствует вещество торий.

Массовое число уменьшится на 4: 238–4 = 234.

Следовательно:

238.92U→234.90Th+42He

Изменчивость постоянной распада

В первом приближении постоянная распада является константой, специфичной для изотопа; более того, наблюдая за этим фактом, Анри Беккерель понял, что радиоактивность — это атомное явление, а не химическое. Однако есть явления, которые незначительно влияют на значение константы.

Под влиянием химического состава

Примеры

Бериллий 7 радиоактивен; относительное изменение его константы распада в зависимости от того, является ли он сам по себе или связан в молекуле F 2 Beсоставляет порядка 0,1  % . Это связано с тем, что фтор, который является очень электроотрицательным, притягивает поверхностные электроны бериллия и, таким образом, сильно изменяет электрическое поле внутри ядра.

Под действием давления

Радиоактивная постоянная слабо, но примерно линейно изменяется с давлением. Таким образом, при давлении 10 8  Па относительное изменение радиоактивной постоянной бериллия 7 составляет примерно 0,0022% . Это явление использовалось для оценки высоких давлений.

• Константа распада полностью ионизированного атома может сильно измениться, поскольку ионизация может способствовать режимам распада. Например, период полураспада полностью ионизированного рения 187 составляет (32,9 ± 2,0) года против 41 миллиарда лет для нейтрального атома, а у полностью ионизированного диспрозия 163 — 47+5 −4 дней, пока нейтральный атом остается стабильным .
• Нейтрон, присутствующий в атомном ядре, намного более стабилен, чем свободный нейтрон, который радиоактивен с периодом полураспада около пятнадцати минут .

Период полураспада радиоактивного вещества

«  Период полураспада  » или период полураспада радиоактивного изотопа — это время, по истечении которого количество ядер этого изотопа, присутствующих в образце, уменьшается вдвое. Обычно обозначается буквой T или t _½ .

Если мы наблюдаем образец радиоактивного материала, через время t _1/2 , этот образец (по определению) потеряет половину своего материала, и останется только половина исходного материала. Но по истечении этого времени дважды потеря дополнительного материала относится только к оставшейся половине, а не к исходной сумме; после двойного t _½ останется половина половины исходного материала, то есть четверть. Точно так же после трехкратного увеличения t _½ останется только (1/2) 3 = 1/8 первоначальной выборки и так далее. После того, как этот период полураспада будет увеличиваться в десять раз, активность снизится в 2 10 = 1024 раза, то есть существенно разделить на тысячу. t _1/2 — время, по истечении которого количество радиоактивных ядер, присутствующих в образце, уменьшается вдвое, но «срок службы» образца намного превышает его «период полураспада»: радиоактивного вещества всегда остается немного, даже после большое количество «периодов полураспада».

Математически закон распада радиоактивного образца можно охарактеризовать следующим образом:

Математическая характеристика периода полураспада и средней продолжительности жизни

Если N (t) представляет собой количество радионуклидов в момент времени t, то:

НЕТ(т12)знак равноНЕТ2знак равноНЕТе-λт12знак равноНЕТепер⁡(12){\ displaystyle N (t_ {1/2}) = {\ frac {N_ {0}} {2}} = N_ {0} e ^ {- \ lambda t_ {1/2}} = N_ {0} e ^ {\ ln (1/2)}}

Сразу выводим:

т12знак равнопер⁡(2)λ{\ displaystyle t_ {1/2} = {\ frac {\ ln (2)} {\ lambda}}}

или же:

λзнак равнопер⁡(2)т12{\ displaystyle \ lambda = {\ frac {\ ln (2)} {t_ {1/2}}}}

где — количество начальных ядер, — радиоактивная постоянная, соответствующая типу ядер.
НЕТ{\ displaystyle N_ {0}}λ{\ displaystyle \ lambda}

Средняя выживаемость

Период полураспада не следует путать со средней продолжительностью t . Это получается с помощью следующих рассуждений: количество ядер, распадающихся в момент t, «проживало» в течение этого времени t или, точнее, в момент t остается N exp (–λ t) ядер. Из них за период времени уничтожаются:

dНЕТзнак равноλНЕТexp⁡(-λт)dт{\ displaystyle dN = \ lambda N_ {0} \ exp (- \ lambda t) dt}.

Следовательно, эти dN имеют срок службы от t до t + dt. Таким образом, мы можем определить среднюю продолжительность жизни всех радионуклидов в выборке (или просто среднюю продолжительность жизни ) следующим образом:

т¯знак равно∫НЕТтdНЕТНЕТ{\ displaystyle {\ overline {t}} = \ int _ {N_ {0}} ^ {0} t {\ frac {dN} {N_ {0}}}}.

Таким образом, учитывая приведенное выше выражение для dN, получаем

т¯знак равноλ∫+∞тexp⁡(-λт)dтзнак равно1λзнак равнот12пер⁡(2)≈1,44 годт12{\ displaystyle {\ overline {t}} = \ lambda \ int _ {0} ^ {+ \ infty} t \ exp (- \ lambda t) dt = {\ frac {1} {\ lambda}} = {\ гидроразрыв {t_ {1/2}} {\ ln (2)}} \ приблизительно 1 {,} 44 \, t_ {1/2}}.

В научной литературе среднее время жизни радиоактивного вещества обычно обозначается греческой буквой τ, поэтому

τзнак равнот¯знак равно1λ{\ displaystyle \ tau = {\ overline {t}} = {\ frac {1} {\ lambda}}}.

Этот срок службы не зависит от размера образца  ; это характерное время рассматриваемого радионуклида, как и его период полураспада . По истечении этого характерного времени τ активность снижается до доли 1 / e от своего начального значения:
НЕТ{\ displaystyle N_ {0}}т12{\ displaystyle t_ {1/2}}

НЕТ(τ)знак равноНЕТexp⁡(-λλ)знак равноНЕТе{\ Displaystyle N (\ тау) = N_ {0} \ ехр (- \ lambda / \ lambda) = {\ frac {N_ {0}} {e}}}.

Можно отметить, что это «время жизни» на самом деле является средним временем выживания атома в образце с начала наблюдения . В случае естественного радионуклида его предыдущая жизнь могла быть намного дольше, иногда составляя миллионы лет и более. Символическим примером является Плутоний 244 , с периодом полураспада 80,8 мега- лет, из которых следы атомов , образованных процессов примитивных звездных взрывов задолго до формирования и эволюции системы находятся в почве Земли. Солнечная , так что там больше 5 Гиг- лет. Эти атомы первоначально имели среднюю выживаемость около 80,8 / Ln (2) = 80,8 x 1,4427 млн ​​лет, или 116,7 миллиона лет; но те, кого мы обнаруживаем сегодня — то немногое, что от них осталось — выжили, по крайней мере, в пятьдесят раз больше. Они выжили благодаря удаче; и в среднем их потенциал выживания, отсчитываемый с сегодняшнего дня, составляет 80,8 мега- лет, как в первый день.

Закон радиоактивного распада

Любой радионуклидный как вероятно, распадаться в любой момент времени в качестве еще одного радионуклида того же вида, и распад не зависит от физико — химических условий , в которых найден нуклид. Другими словами, распад управляется случайностью, а закон радиоактивного распада — это статистический закон .

NB: в деталях, непрерывные измерения, кажется, показывают вариации радиоактивного распада в зависимости от скорости воздействия нейтрино, которая незначительно меняется в зависимости от положения Земли по отношению к Солнцу.

Если образец радиоактивного материала наблюдается в течение заданного интервала времени, доля ядер, подвергающихся радиоактивному распаду, будет практически постоянной из-за закона больших чисел .

Это показывает , что математически это означает , что число N ядер уменьшается со временем т после экспоненциального распада  : . Это демонстрируется следующим образом:
НЕТ(т)знак равноНЕТе-λт{\ Displaystyle N (T) = N_ {0} \, e ^ {- \ lambda t}}

Математическая демонстрация экспоненциального закона

Пусть Н ( т ) быть количество радионуклидов одного данного химического элемента , присутствующего в образце , в любой момент времени т . Поскольку вероятность распада одного из этих радионуклидов не зависит ни от присутствия других радионуклидов, ни от окружающей среды, общее количество распадов –d N за небольшой интервал времени d t ( N уменьшается со временем: d N — изменение числа N (d N <0), количество недостающих ядер равно –d N ) пропорционально количеству радионуклидов N, присутствующих в момент времени t, и продолжительности d t этого интервала:

-dНЕТзнак равноλНЕТdт{\ displaystyle — \ mathrm {d} N = \ lambda N \, \ mathrm {d} t}

где коэффициент пропорциональности λ , называемый радиоактивной постоянной рассматриваемого радионуклида, имеет размерность, обратную времени; постоянная λ положительна.

Интегрируя предыдущее дифференциальное уравнение, мы находим число N ( t ) радионуклидов, присутствующих в организме в любой момент t , зная, что в данный момент t = 0 их было N  ; это экспоненциальный закон затухания

НЕТ(т)знак равноНЕТе-λт{\ Displaystyle N (T) = N_ {0} \, e ^ {- \ lambda t}}

или же :

• N — начальное количество неразложившихся ядер;
• λ — радиоактивная постоянная элемента.

Однако следует отметить, что этот закон уменьшения касается только радиоактивности, вызванной исходным радионуклидом  ; но радионуклиды, образующиеся в результате радиоактивного распада исходного радионуклида, могут сами быть радиоактивными и вызывать свою собственную радиоактивность. В этом случае их радиоактивность постепенно добавляется к радиоактивности исходного радионуклида. Активность смеси, созданной таким образом между исходным радионуклидом и его потомком (ями), обсуждается в разделе «Филиализация двух зависимых изотопов» ниже.

Энергия связи нуклонов в ядре. Ядерные силы

Между нуклонами ядра действуют самые мощные силы природы – ядерные силы.

Ядерные силы – это силы притяжения, связывающие протоны и нейтроны в атомном ядре и обеспечивающие существование устойчивых ядер.

Свойства ядерных сил:

• являются силами притяжения;
• являются короткодействующими силами (действуют на малых расстояниях, не превышающих 2·10-15 м; на таком расстоянии ядерные силы больше кулоновских приблизительно в 100 раз);
• обладают свойством зарядовой независимости (ядерные силы, действующие между двумя протонами, двумя нейтронами и между протоном и нейтроном, одинаковы);
• имеют свойство насыщения (каждый нуклон взаимодействует только с ограниченным числом ближайших к нему нуклонов, а не со всеми нуклонами ядра);
• не являются центральными (не действуют по линии, соединяющей центры взаимодействующих нуклонов).

Массу ядра можно точно определить с помощью масс-спектрографов, которые разделяют заряженные частицы с разными удельными зарядами с помощью электрических и магнитных полей.

Опытным путем было установлено, что благодаря действию сил притяжения масса ядра всегда меньше суммы масс протонов и масс нейтронов, входящих в состав этого ядра:

где ​\( M \)​ – масса ядра.

Дефект масс – это величина, равная разности суммы масс входящих в ядро нуклонов и массы ядра:

где ​\( \Delta m \)​ – дефект масс.

Благодаря ядерным силам ядра атомов обладают огромной энергией связи.

Энергия связи – это энергия, которую необходимо затратить, чтобы разделить ядро на составляющие его нуклоны, или энергия, которая выделяется при образовании ядра из отдельных нуклонов:

где ​\( \Delta E_{св} \)​ – энергия связи, ​\( c \)​ – скорость света.

Если в формуле энергии связи массы протона и нейтрона выражены в килограммах, а скорость света – в метрах в секунду, то энергия связи будет измерена в джоулях. Однако в физике атома и атомного ядра энергию ядер и элементарных частиц чаще выражают в мегаэлектронвольтах (МэВ).

Энергетический эквивалент 1 а.е.м.

Поэтому энергию связи можно рассчитать следующим образом:

В этом случае энергия связи измеряется в мегаэлектронвольтах (МэВ).

Для характеристики прочности ядра используется величина, которая называется удельной энергией связи.

Удельная энергия связи – это энергия связи ядра, приходящаяся на один нуклон ядра:

где ​\( A \)​ – массовое число.

Удельная энергия связи неодинакова для разных химических элементов и даже для изотопов одного и того же химического элемента. Удельная энергия связи нуклона в ядре меняется в среднем в пределах от 1 МэВ у легких ядер до 8,6 МэВ у ядер средней массы (с массовым числом ​\( A \)​ ≈ 100). У тяжелых ядер (​\( A \)​ ≈ 200) удельная энергия связи нуклона меньше, чем у ядер средней массы, приблизительно на 1 МэВ, так что их превращение в ядра среднего веса (деление на 2 части) сопровождается выделением энергии в количестве около 1 МэВ на нуклон, или около 200 МэВ на ядро. Превращение легких ядер в более тяжелые ядра дает еще больший энергетический выигрыш в расчете на нуклон.

Зависимость удельной энергии связи от массового числа установили экспериментально. Из рисунка хорошо видно, что, не считая самых легких ядер, удельная энергия связи примерно постоянна и равна 8 МэВ/нуклон. Отметим, что энергия связи электрона и ядра в атоме водорода, равная энергии ионизации, почти в миллион раз меньше этого значения. Кривая на рисунке имеет слабо выраженный максимум. Максимальную удельную энергию связи (8,6 МэВ/нуклон) имеют элементы с массовыми числами от 50 до 60, т. е. железо и близкие к нему по порядковому номеру элементы. Ядра этих элементов наиболее устойчивы.

У тяжелых ядер удельная энергия связи уменьшается за счет возрастающей с увеличением ​\( Z \)​ кулоновской энергии отталкивания протонов. Кулоновские силы стремятся разорвать ядро.

Закон радиоактивного распада и единицы радиоактивности

При изучении явления радиоактивности было установлено, что с течением времени количество радиоактивных атомов уменьшается. Оно может происходить как очень быстро (доли секунды), так и очень медленно (миллионы и миллиарды лет).

При этом скорость уменьшения числа атомов является характерной особенностью для каждого радионуклида.

Поэтому, за единицу времени распадается всегда одна и та же доля радиоактивных атомов, независимо от их первоначального количества.

Эта закономерность получила название закона радиоактивного распада. Доля атомов элемента, распадающихся за единицу времени, получила название постоянной распада (λ–лямбда). Она измеряется в единицах, обратных времени (сек -1, ч -1, сут -1, млрд. лет -1 и т.д.).

Кроме величины λ для характеристики данного закона также используется другая величина – период полураспада (Т_1/2) – которую ввел в науку Э. Резерфорд (1900). Это время, в течение которого количество радиоактивных атомов уменьшается в два раза, т.е. наполовину.

Таким образом, радиоактивность прямо пропорциональна числу ядерных распадов за единицу времени (λ) и обратно пропорциональна периоду полураспада (Т_1/2).

Считается, что полный распад любого радиоизотопа занимает промежуток времени, равный 10 Т_1/2. Хотя на самом деле всегда остается ничтожно малое количество изотопа, который может образоваться за счет распада других материнских элементов.

Действие ионизирующих излучений представляет собой сложный процесс. Эффект облучения зависит от величины поглощенной дозы, ее мощности, вида излучения, объема облучения тканей и органов.

Для его количественной оценки введены специальные единицы, которые делятся на внесистемные и единицы в системе СИ. Сейчас используются преимущественно единицы системы СИ.

В качестве абсолютной единицы измерения радиоактивности (А) в системе СИ (SI) выбран беккерель (Бк, Bq), равный одному распаду в секунду.

Однако ввиду очень малого значения для выражения больших уровней радиоактивности параллельно этой системной единице применяют и внесистемную – кюри (Ки, Ci), равную 37 млрд. распадов в секунду. Эта величина выражает радиоактивность 1 г Ra226, предложенного в 1911 г. Марией Склодовской-Кюри в качестве эталонного источника.

Наряду с этим для измерения радиоактивности применяются различные кратные и дольные приставки (табл. 1).

Таблица 1. Приставки СИ для образования наименований десятичных кратных и дольных единиц

Приставка	Обозначение	Множитель	Пример
экса	Э	1018	эксабеккерель, ЭБк
пета	П	1015	петакюри, ПКи
тера	Т	1012	терабеккерель, ТБк
гига	Г	109	гигакюри, ГКи
мега	М	106	мегабеккерель, МБк
кило	к	103	килобеккерель, кБк
гекто	г	102	гектокюри, гКи
дека	да	101	декабеккерель, даБк
деци	д	10-1	децикюри, дКи
санти	с	10-2	сантикюри, сКи
милли	м	10-3	милликюри, мКи
микро	мк	10–6	микрокюри, мкКи
нано	н	10-9	нанокюри, нКи
пико	п	10-12	пикокюри, пКи
фемто	ф	10-15	фемтокюри, фКи
атто	а	10-18	аттокюри, аКи

Различают массовую, поверхностную и объемную удельную радиоактивность.

Массовая удельная радиоактивность- это отношение числа радиоактивных распадов за 1 секунду к единице массы пробы. Например,  Бк или Ки/г, кг, ц, т и.т.д.

Поверхностная удельная радиоактивность – это отношение числа радиоактивных распадов за одну секунду к единице площади пробы. Например, Ки или Бк/см2, м2, км2, га и т.д.

И, наконец, объемная удельная радиоактивность – это отношение числа радиоактивных распадов за одну секунду к единице объема пробы. Например, Бк или Ки /cм3, мл, л, м3 и т.д.

Предыдущая

Примечания и ссылки

Заметки

1. Для этого определения предполагается, что образец не содержит никаких радиоизотопов, кроме рассматриваемого. Активность образца, содержащего несколько радиоизотопов, является суммой их соответствующих активностей.
2. На самом деле калий 40 может быть преобразован в аргон 40 двумя способами: большую часть времени захватом электронов, но также и , примерно один раз из десяти тысяч. Каждый из двух вариантов, приводящих к аргону 40, характеризуется своей собственной константой распада. Если вы не хотите , чтобы пренебрегать любой вариант мы пишем: .λзнак равноλ1+λ2+λ3{\ displaystyle \ lambda = \ lambda _ {1} + \ lambda _ {2} + \ lambda _ {3}}

Рекомендации

1. ↑ и Даниэль Блан, Precis of Nuclear Physics , Dunod ,2003 г.( 1- е  изд. 1993 г.), гл.  5 («Естественная радиоактивность, искусственная радиоактивность»), с.  65–66.
2. Бернар Фернандес, От атома к ядру: исторический подход к атомной физике и ядерной физике , Эллипсы ,2006 г., 597  с. ( ISBN  978-2729827847 ) , часть I, гл.  1 («Лучи Беккереля»), с.  9.
3. (in) О. Клеппер , »  Измерение бета-распада связанного состояния и времени жизни ядра в ЭПР накопительно-охладительного кольца  » , Nuclear Physics A , vol.  626, н.у.к. .  1-2,Ноябрь 1997 г., стр.  199–213 .
4. (о) Ф. Бош , Т. Faestermann , Дж Фриз , Ф. Хейне , П. Кини , Е. Wefers , К. Zeitelhack , К. Беккерт , Б. Franzke , О. Klepper , С. Кожухары , Г. Менцель , Р. Moshammer , Ф. Nolden , Х. Рейч , Б. Schlitt , М. Steck , Т. Stöhlker , Т. Уинклер и К. Такахаши , «  Наблюдение связанного состояния р — распад полностью ионизированной 187 Re: 187 Re — 187 Os Cosmochronometry  » , Physical Review Letters , том.  77, п о  26,1996 г., стр.  5190–5193 ( PMID   , DOI   , Bibcode   ).
5. (in) Мистер Юнг и Ф. Бош, К. Бекерт, Х. Айкхофф, Х. Фольгер, Б. Францке, А. Грубер, П. Кинле, О. Клеппер, В. Кениг, К. Кожухаров, Р. Манн, Р. Moshamnler, Ф. Nolden, У. Шааф, Г. Soff, П. Spadtke, М. Steck, Th Stohlker и К. Summerer,. «  Первое наблюдение связанного состояния бета — распад  » , Physical Review Letters , полет.  69, п о  15,1992 г., стр.  2164–2167 .

• Физический портал
• Химический портал
• Ядерный портал

Вопросы на тему «Радиоактивность»

Вопрос 1. Что такое радиоактивность?

Ответ. Радиоактивностью называют способность некоторых нестабильных атомных ядер самопроизвольно превращаться в другие ядра с испусканием частиц. Испускание (или излучение) таких частиц называется радиоактивным излучением.

Вопрос 2. Какие частицы излучаются при превращении ядер?

Ответ. Различают превращения ядер с излучением α (альфа)-частиц, β (бета)-частиц (электронов) и сопровождающихся γ(гамма)-излучением.

Вопрос 3. Когда было открыто явление радиоактивности?

Ответ. Явление радиоактивности было открыто в 1896 году французским физиком Анри Беккерелем.

До Беккереля французский исследователь Ньепс де Сен-Виктор в промежутке между 1856 и 1861 в своих экспериментах предполагал, что соли урана испускают какое-то невидимое для человеческого глаза излучение.Тогда эти сообщения не были восприняты научным сообществом, и первооткрывателем явления принято считать Беккереля. 

Вопрос 4. Что такое атомное ядро?

Ответ. Ядром называется центральная часть атома, в которой сосредоточена практически вся масса атома и его положительный электрический заряд. Все атомные ядра состоят из элементарных частиц: протонов и нейтронов, которые считаются двумя зарядовыми состояниями одной частицы — нуклона. Протон имеет положительный электрический заряд, равный по абсолютной величине заряду электрона. Нейтрон не имеет электрического заряда.

Радий стал популярен и в начале XX века, даже считался полезным и включался в состав многих продуктов питания и бытовых предметов: хлеб, шоколад, питьевая вода, зубная паста, краска для циферблатов наручных часов. Однако впоследствии выяснилось, что радий чрезвычайно радиотоксичен, и использование его было остановлено.

Вопрос 5. Что такое изотопы и изобары?

Ответ. Ядра с одинаковыми Z, но различными А называются изотопами. Ядра, которые при одинаковом А имеют различные Z, называются изобарами.

Нужна помощь в решении задач? Обращайтесь в профессиональный сервис для студентов в любое время!