Зачем нужно шифрование?

Введение

Наверняка вы сталкивались с таким понятием, как «электронная подпись». Если обратиться к федеральному закону, то можно найти следующее её определение:

Для меня, как для человека, редко работающего с подобного рода документами, определение несколько абстрактное, хоть и отражает суть ЭП — определение лица, подписавшего некоторый документ. Помимо этого, ЭП может быть использована для определения искажений переданного сообщения, в чём мы сможем убедиться позднее.

Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.

Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.

Хеш-функции

Хешированием (от англ. hash) называется преобразование исходного информационного массива произвольной длины в битовую строку фиксированной длины.

Алгоритмов хеш-функций немало, а различаются они своими характеристиками – криптостойкостью, разрядностью, вычислительной сложностью и т.д.

Нас интересуют криптографически стойкие хеш-функции. К таким обычно предъявляют два требования:

• Для заданного сообщения С практически невозможно подобрать другое сообщение С’ с таким же хешем
• Практически невозможно подобрать пар сообщений (СС’), имеющих одинаковый хеш.

Требования называются стойкостью к коллизиям первого рода и второго рода соответственно.
Для таких функций остается важным и другое требование: при незначительном изменении аргумента должно происходить значительное изменение самой функции. Таким образом, значение хеша не должно давать информации даже об отдельных битах аргумента.

Примеры хеш-алгоритмов

• Adler-32
• CRC
• SHA-1
• SHA-2 (SHA-224, SHA-256, SHA-384, SHA-512)
• HAVAL
• MD2
• MD4
• MD5

• N-Hash

• RIPEMD-256
• RIPEMD-320
• Skein
• Snefru
• Tiger (TTH)
• Whirlpool
• ГОСТ Р34.11-94 (ГОСТ 34.311-95)
• IP Internet Checksum (RFC 1071)

Cryptomator

Cryptomator является полностью открытым исходным кодом и работает с Windows, Mac и Linux. Он использует технологию под названием «Прозрачное шифрование», что означает, что вы вряд ли заметите разницу в работе с вашими файлами. Он создает виртуальный жесткий диск для всех ваших файлов, находящихся в облачном хранилище, и шифрует их для безопасного доступа.

Самое замечательное, что вам не нужно изучать какие-либо сложные рабочие процессы или функции, чтобы сделать эту работу. Cryptomator разработан таким образом, что позволяет вам шифровать и получать доступ к вашим файлам так же, как вы бы делали это без него.

Поскольку это программное обеспечение с открытым исходным кодом, вы можете оплатить любую сумму, которую хотите загрузить. На самом деле, вы можете скачать его бесплатно.

Теперь пришло время одноключевых КА.

DES

• ECB (англ. electronic code book) — режим «электронной кодовой книги» (простая замена);
• CBC (англ. cipher block chaining) — режим сцепления блоков;
• CFB (англ. cipher feed back) — режим обратной связи по шифротексту;
• OFB (англ. output feed back) — режим обратной связи по выходу.
• Прямым развитием DES в настоящее время является алгоритм Triple DES (3DES). В 3DES шифрование/расшифровка выполняются путём троекратного выполнения алгоритма DES.

RC4

• высокая скорость работы;
• переменный размер ключа.

• используются не случайные или связанные ключи;
• один ключевой поток используется дважды.

Illivion

Blowfish

1. скорость (шифрование на 32-битных процессорах происходит за 26 тактов);
2. простота (за счёт использования простых операций, уменьшающих вероятность ошибки реализации алгоритма);
3. компактность (возможность работать в менее, чем 5 Кбайт памяти);
4. настраиваемая безопасность (изменяемая длина ключа).

Twofish

1. 128-битный блочный симметричный шифр
2. Длина ключей 128, 192 и 256 бит
3. Отсутствие слабых ключей
4. Эффективная программная (в первую очередь на 32-битных процессорах) и аппаратная реализация
5. Гибкость (возможность использования дополнительных длин ключа, использование в поточном шифровании, хэш-функциях и т. д.).
6. Простота алгоритма — для возможности его эффективного анализа.

Skipjack

Принимая во внимание, что стоимость вычислительных мощностей уменьшается вдвое каждые 18 месяцев, лишь через 36 лет стоимость взлома Skipjack полным перебором сравняется со стоимостью взлома DES сегодня.
Риск взлома шифра с помощью более быстрых способов, включая дифференциальный криптоанализ, незначителен. Алгоритм не имеет слабых ключей и свойства комплементарности.
Устойчивость Skipjack к криптоанализу не зависит от секретности самого алгоритма.

Mars

• простейшие операции (сложение, вычитание, исключающее или)
• подстановки с использованием таблицы замен
• фиксированный циклический сдвиг
• зависимый от данных циклический сдвиг
• умножение по модулю 232
• ключевое забеливание

Idea

• сложение по модулю
• умножение по модулю
• побитовое исключающее ИЛИ (XOR).

• никакие две из них не удовлетворяют дистрибутивному закону
• никакие две из них не удовлетворяют ассоциативному закону

Folder Lock

При загрузке более 56 Кб Folder Lock позволяет шифровать данные и папки для последующего безопасного совместного использования. Он получил несколько наград и был высоко оценен на таких платформах, как CNET и Softonic. В дополнение к традиционным функциям программного обеспечения для шифрования, Folder Lock позволяет:

• Защита паролем USB / внешние накопители
• Навсегда удалять файлы
• Очистить историю Windows
• Включить stealth режим
• Резервное копирование зашифрованных файлов на защищенном облачном сервере

Он доступен на нескольких разных языках, и вы можете скачать его бесплатно, чтобы опробовать основные функции.

Стандартные шифры

ROT1

Этот шифр известен многим детям. Ключ прост: каждая буква заменяется на следующую за ней в алфавите. Так, А заменяется на Б, Б — на В, и т. д. Фраза «Уйрйшоьк Рспдсбннйту» — это «Типичный Программист».

Попробуйте расшифровать сообщение:

Шифр транспонирования

В транспозиционном шифре буквы переставляются по заранее определённому правилу. Например, если каждое слово пишется задом наперед, то из hello world получается dlrow olleh. Другой пример — менять местами каждые две буквы. Таким образом, предыдущее сообщение станет eh ll wo ro dl.

Серия вебинаров AWS «Как обезопасить данные в облаке»

18 октября – 1 ноября, Онлайн, Беcплатно

tproger.ru

События и курсы на tproger.ru

Ещё можно использовать столбчатый шифр транспонирования, в котором каждый символ написан горизонтально с заданной шириной алфавита, а шифр создаётся из символов по вертикали. Пример:

Из этого способа мы получим шифр holewdlo lr. А вот столбчатая транспозиция, реализованная программно:

Азбука Морзе

В азбуке Морзе каждая буква алфавита, цифры и наиболее важные знаки препинания имеют свой код, состоящий из череды коротких и длинных сигналов:Чаще всего это шифрование передаётся световыми или звуковыми сигналами.

Сможете расшифровать сообщение, используя картинку?

Шифр Цезаря

Это не один шифр, а целых 26, использующих один принцип. Так, ROT1 — лишь один из вариантов шифра Цезаря. Получателю нужно просто сообщить, какой шаг использовался при шифровании: если ROT2, тогда А заменяется на В, Б на Г и т. д.

А здесь использован шифр Цезаря с шагом 5:

Моноалфавитная замена

Коды и шифры также делятся на подгруппы. Например, ROT1, азбука Морзе, шифр Цезаря относятся к моноалфавитной замене: каждая буква заменяется на одну и только одну букву или символ. Такие шифры очень легко расшифровываются с помощью частотного анализа.

Например, наиболее часто встречающаяся буква в английском алфавите — «E». Таким образом, в тексте, зашифрованном моноалфавитным шрифтом, наиболее часто встречающейся буквой будет буква, соответствующая «E». Вторая наиболее часто встречающаяся буква — это «T», а третья — «А».

Однако этот принцип работает только для длинных сообщений. Короткие просто не содержат в себе достаточно слов.

Шифр Виженера

Представим, что есть таблица по типу той, что на картинке, и ключевое слово «CHAIR». Шифр Виженера использует принцип шифра Цезаря, только каждая буква меняется в соответствии с кодовым словом.

В нашем случае первая буква послания будет зашифрована согласно шифровальному алфавиту для первой буквы кодового слова «С», вторая буква — для «H», etc. Если послание длиннее кодового слова, то для (k*n+1)-ой буквы, где n — длина кодового слова, вновь будет использован алфавит для первой буквы кодового слова.

Чтобы расшифровать шифр Виженера, для начала угадывают длину кодового слова и применяют частотный анализ к каждой n-ной букве послания.

Попробуйте расшифровать эту фразу самостоятельно:

Подсказка длина кодового слова — 4.

Шифр Энигмы

Энигма — это машина, которая использовалась нацистами во времена Второй Мировой для шифрования сообщений.

Есть несколько колёс и клавиатура. На экране оператору показывалась буква, которой шифровалась соответствующая буква на клавиатуре. То, какой будет зашифрованная буква, зависело от начальной конфигурации колес.

Существовало более ста триллионов возможных комбинаций колёс, и со временем набора текста колеса сдвигались сами, так что шифр менялся на протяжении всего сообщения.

Откуда взялась идея создания системы с открытым ключом

Вопросы о безопасном шифровании стали возникать еще в начале 70-х годов. Именно в это время криптографии и математики признали, что асимметричное шифрование по ключу возможно. Самая успешная модель создания зашифрованного послания заключалась в следующих шагах:

• отправитель пишет сообщение и зашифровывает его собственным ключом;
• полученный криптографический текст он направляет абоненту;
• принимающий, получив зашифрованное сообщение, ещё раз его, шифрует собственным ключом и обратно присылает отправителю;
• получив от принимающего дважды зашифрованное сообщение отправитель расшифровывает его наполовину своим ключом и отправляет обратно;
• принимающий расшифровывает послание своим ключом и получает читаемый открытый текст.

Метод был предложен в начале 70-х годов Диффи и Хелманном. Позже, описанная выше модель шифрования позволила учёным криптологам  разрушить миф о невозможности применения ассиметричного метода для кодирования сообщений открытым способом.

Описания алгоритма шифрования

Давайте теперь перейдем от математики к описанию самого алгоритма шифрования AES c размером ключа 128 бит.

Предварительно входные данные разбиваются на блоки по 16 байт, если полный размер не кратен 16 байтам, то данные дополняется до размера, кратного 16 байтам. Блоки представляются в виде матрицы 4×4 — state. Далее происходит процедура расширения ключа и к каждому блоку state применяются операции 2-4. Итак, алгоритм состоит из следующих шагов:

1. Расширение ключа — KeyExpansion;

2. Начальный раунд — сложение state с основным ключом;

3. 9 раундов шифрования, каждый из которых состоит из преобразований:

   · SubBytes

   · ShiftRows

   · MixColumns

   · AddRoundKey

4. Финальный раунд, состоящий из преобразований:

   · SubBytes

   · ShiftRows

   · AddRoundKey

Рассмотрим подробнее каждое из представленных выше преобразований:

SubBytes — замена байтов state по таблице S-box. Каждый байт представляется в виде двух шестнадцатеричных чисел b = (x, y), где x определяется 4 старшими разрядами b, а y — 4 младшими. В таблице S-box размера 16×16 находятся значения для замены исходного байта: значение b’ на пересечении строки x и столбца y S-box используется в качестве замены исходному байту b.

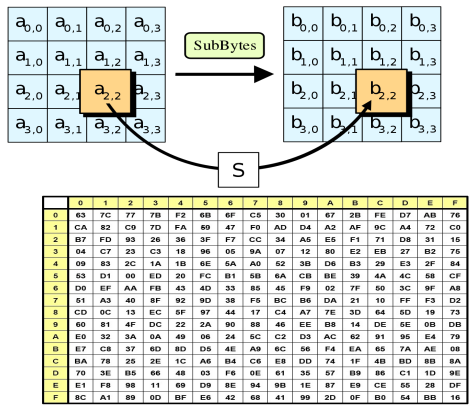
ShiftRows — циклический сдвиг строк state. Нулевая строка остается на месте, первая смещается влево на 1 байт, вторая на 2 байта и третья на 3 соответственно.

MixColumns — умножения каждого столбца state на фиксированную матрицу. Таким образом осуществляется линейное преобразование над столбцами state. Причем умножение и сложение производится по правилам, описанным выше.

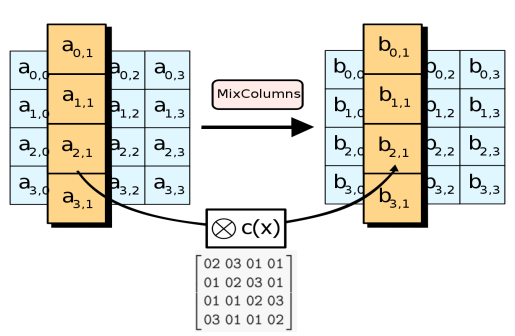
AddRoundKey — раундовый ключ поэлементно добавляется к state с помощью поразрядного XOR.

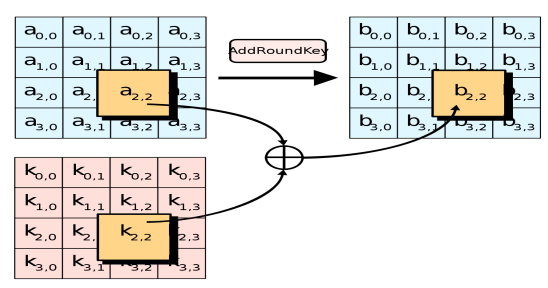
• KeyExpansion — процедура расширения основного ключа для создания раундовых ключей, которые затем используются в раундах шифрования. Расширенный ключ состоит из 44 четырехбайтовых слов (w_i): 4 слова на основной ключ и по 4 слова на 10 раундовых ключей. Таким образом, полная длина расширенного ключа составляет 1408 бит.

  Операция расширения ключа использует массив Rcon и состоит из следующих действий:

  • Четыре слова основного ключа переносятся в первые четыре слова расширенного ключа.

  • Если число i без остатка делится на 4, то w_i =SubBytes(RotByte(w_i-1 )) xor Rcon_i/4 .

  • Иначе: w_i = w_i-4 xor w_i-1 .

Операция RotByte производит циклическую перестановку байта исходного слова: { x, x₁, x₂, x₃ } → { x₃ , x , x₁ , x₂ }.

Ниже показан пример, демонстрирующий генерацию 2 первых слов первого раундового ключа.

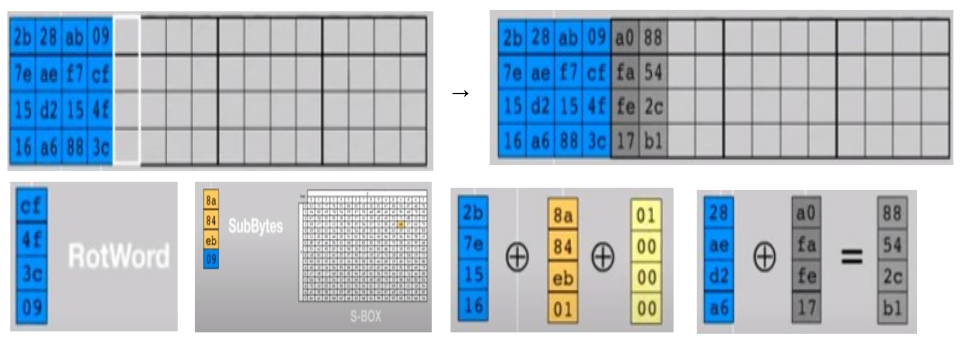https://www.youtube.com/watch?v=CxU4ROAYGzs

История

Использовавшийся в Древней Греции шифр «скитала», чья современная реконструкция показана на фото, вероятно был первым устройством для шифрования *Скитала — древний принцип шифровки данных при помощи бумаги. Палку обворачивали бумагой, писали слово на свёртке, и заполняли пустые места случайными символами Роторная шифровальная машина Энигма, разные модификации которой использовались немецкими войсками с 1929 года до конца Второй мировой войны Основная статья: История криптографии

История криптографии насчитывает около 4 тысяч лет. В качестве основного критерия периодизации криптографии возможно использовать технологические характеристики используемых методов шифрования.

Первый период (приблизительно с 3-го тысячелетия до н. э.) характеризуется господством моноалфавитных шифров (основной принцип — замена алфавита исходного текста другим алфавитом через замену букв другими буквами или символами). Второй период (хронологические рамки — с IX века на Ближнем Востоке (Ал-Кинди) и с XV века в Европе (Леон Баттиста Альберти) — до начала XX века) ознаменовался введением в обиход полиалфавитных шифров. Третий период (с начала и до середины XX века) характеризуется внедрением электромеханических устройств в работу шифровальщиков. При этом продолжалось использование полиалфавитных шифров.

Четвёртый период — с середины до 70-х годов XX века — период перехода к математической криптографии. В работе Шеннона появляются строгие математические определения количества информации, передачи данных, энтропии, функций шифрования. Обязательным этапом создания шифра считается изучение его уязвимости для различных известных атак — линейного и дифференциального криптоанализа. Однако, до 1975 года криптография оставалась «классической», или же, более корректно, криптографией с секретным ключом.

Современный период развития криптографии (с конца 1970-х годов по настоящее время) отличается зарождением и развитием нового направления — криптография с открытым ключом. Её появление знаменуется не только новыми техническими возможностями, но и сравнительно широким распространением криптографии для использования частными лицами (в предыдущие эпохи использование криптографии было исключительной прерогативой государства). Правовое регулирование использования криптографии частными лицами в разных странах сильно различается — от разрешения до полного запрета.

Современная криптография образует отдельное научное направление на стыке математики и информатики — работы в этой области публикуются в научных журналах, организуются регулярные конференции. Практическое применение криптографии стало неотъемлемой частью жизни современного общества — её используют в таких отраслях как электронная коммерция, электронный документооборот (включая цифровые подписи), телекоммуникации и других.

Виды асимметричного шифрования

В настоящее время действует более 10 систем шифрования асимметричным методом. Самая распространенная это RSA. Алгоритм, часто применяется для защиты программного обеспечения, с использованием схем цифровой подписи.

DSA ещё один метод, который позволяет создать цифровую подпись публичного типа с возможностью проверки данных.

Elgamal распространенный в России способ проверки цифровой подписи. Разработанный алгоритм надёжно защищает ресурс от компрометации. В 1994 году был создан ГОСТ Р 34.10-94. На его основе был разработан собственный метод шифрования асимметричным способом в виде ГОСТ Р 34.10-2012.

Полное шифрование диска

Для того, чтобы лучше защитить все данные (включая файлы операционной системы) на жестком диске вашего компьютера от несанкционированного доступа третьих лиц, лучше использовать шифрование всего диска.

Он заключается в обеспечении доступа к компьютеру с использованием ключа. Это может быть обычный пароль, который необходимо запомнить, модуль TPM, файл на флешке или биометрический считыватель.

Важно, что ключ шифрования должен быть введен еще до загрузки операционной системы, потому что файлы были закодированы и нечитаемы для загрузчика. Без знания пароля или ключа мы не получим доступа к компьютеру. Перенос диска на другой компьютер также ничего не даст, потому что весь диск зашифрован – кроме небольшого раздела, ответственного за принятие ключа и дешифрацию

Это метод защищает не только данные пользователей, но и файл подкачки и временные коллекции, из которых можно было бы извлечь секретную информацию. Кроме того, мы скрываем структура каталогов, имена файлов, их размеры, метаданные. Благодаря методу полного шифрования дисков, мы защищаем все данные, а не только выбранные файлы.

Такой способ, однако, имеет недостатки. Для полного шифрования диска можно использовать бесплатный инструмент под названием VeraCrypt, разработанный на основе программы TrueCrypt. Но, к сожалению, в некоторых случаях применение только шифрования может представлять опасность, например, когда кто-то получит доступ к включенному компьютеру. Поэтому стоит наиболее ценные данные дополнительно шифровать на уровне файлов.

Вернемся к математике

Идея с ящиком, о которой я описывал выше, вдохновили Диффи и Хеллмана искать способ передачи сообщения. В конце концов они пришли к использованию односторонних функций.

Что такое односторонняя функция? К примеру есть функция удвоение, т.е удвоить(4)=8, она двухсторонняя, т.к. из результата 8 легко получить исходное значение 4. Односторонняя функция — та функция после применения которой практически невозможно получить исходное значение. К примеру смешивание желтой и синей краски — пример односторонней функции. Смешать их легко, а вот получить обратно исходные компоненты — невозможно. Одна из таких функций в математике — вычисление по модулю.

За основу алгоритма Хеллман предложил функцию Yx (mod P). Обратное преобразование для такой функции очень сложно, и можно сказать что, по сути, заключается в полном переборе исходных значений.

К примеру вам сказали, что 5 x (mod 7) = 2, попробуйте найдите x, а? Нашли? А теперь представьте что за Y и P взяты числа порядка 10300.

Кстати сказать, для повышения стойкости, число P должно являться простым числом, а Y — являться первообразным корнем по модулю P. Но так как мы все же пытаемся понять теорию, то смысла заморачиваться на этом я не вижу.

Симметричные криптоалгоритмы

Если говорить упрощённо, то симметричные алгоритмы шифрования применяют один ключ для шифрования и дешифрования. Таких алгоритмов много, и на практике обычно применяют те, которые имеют достаточную длину ключа и ещё не были скомпрометированы. Симметричные алгоритмы делятся на блочные (DES, RC2, Blowfish, AES, «Кузнечик» и т. д.) и потоковые (RC4, SEAL, CryptMT и другие).

Стойкость к взлому у всех блочных криптографических алгоритмов во многом определяется длиной ключа. Если она составляет 128 бит и более, шифрование считается сильным, так как для расшифровки информации без ключа потребуются годы работы на мощных компьютерах. Кому любопытно — об алгоритмах шифрования с точки зрения длины ключа можно прочитать в посте на Хабре.

Попрактикуемся: при помощи пакета openssl зашифруем созданный нами ранее текстовый файл. Для этого используем команду:

openssl enc -e -aes256 -in simpletext.txt -out simple_enc_text.txt

где:

• enc — указывает модуль для шифрования;
• -e — указывает, что файлы нужно шифровать;
• -aes256 — алгоритм шифрования;
• -in — указывает на исходный файл;
• -out — указывает на зашифрованный файл.

Выглядит это так:

Для расшифровки нужно указать введённый при шифровании ключ и используемый алгоритм. Команда примерно следующая:

openssl enc -d-aes256 -in simple_enc_text.txt -out simpletext.txt 

где:

• enc — указывает модуль для шифрования;
• -d — указывает, что файлы нужно расшифровать;
• -aes256 — алгоритм шифрования;
• -in — указывает на исходный файл;
• -out — указывает на расшифрованный файл.

При шифровании симметричными алгоритмами есть несколько интересных проблем.

• Длина ключа. Как уже упоминали, желательно не менее 128 бит
• Сложность использования при большом количестве шифруемых объектов — приходится запоминать много параметров.
• Сложность обмена параметрами шифрования (паролями, алгоритмами и подобным) — необходимо обеспечить их надёжную передачу адресату.

Такие проблемы обычно решают при помощи асимметричных алгоритмов шифрования.

Вывод

Это время было богато как на шифры, так и на шифромашины. Впервые появляются не только механические, но и электромеханические шифровальные устройства. С развитием математики, появлением теории чисел и теории вероятности появляются шифры имеющие под собой математическое обоснование. Огромный толчек к развитию криптографии дали частые войны и особенно Первая и Вторая Мировые войны. Фундамент современной криптографии заложен, но это уже другая история…

Переход к математической криптографии

После Первой мировой войны правительства стран засекретили все работы в области криптографии. К началу 1930-х годов окончательно сформировались разделы математики, являющиеся основой для будущей науки — общая алгебра, теория чисел, теория вероятностей и математическая статистика. К концу 1940-х годов построены первые программируемые счётные машины, заложены основы теории алгоритмов, кибернетики. Наибольший прогресс в криптографии достигается в военных ведомствах.

Ключевой вехой в развитии криптографии является фундаментальный труд Клода Шеннона «Теория связи в секретных системах». В этой работе, по мнению многих современных криптографов, был впервые показан подход к криптографии в целом как к математической науке. Были сформулированы её теоретические основы и введены основные понятия.

В 1960-х годах начали появляться различные блочные шифры, которые обладали большей криптостойкостью по сравнению с результатом работы роторных машин. Однако они предполагали обязательное использование цифровых электронных устройств — ручные или полумеханические способы шифрования уже не использовались.

Классическая криптография использовала симметричные алгоритмы шифрования. Шифрование и дешифрование отличаются в таких алгоритмах только порядком выполнения операций. Алгоритмы всегда используют один и тот же секретный элемент — закрытый ключ. Каждый из участников обмена, зная ключ, может как зашифровать, так и расшифровать сообщение.

Существовала несколько проблем связанных с таким подходом:
Первая состоит в том, что классическая схема шифрования прекрасно работает только, пока между участниками информационного обмена есть взаимное доверие. Если же его нет, то могут возникать различные коллизии, так как из-за полной симметрии схемы в случае конфликта между сторонами для независимого наблюдателя нет возможности сделать однозначный вывод, кто из двух участников прав. А если участников не два, а больше, то проблема доверия возрастает в разы.

Второй проблемой являлась проблема передачи шифрующего ключа. Так как современная криптография полагает, что шифрующий ключ нужно постоянно менять, то для этого следует иметь надежный канал связи для передачи ключа. Если передачу ключа нужно осуществить в пределах одного города, то проблем не возникало, а если ключ надо передать в другую страну, то это представляло собой уже сложную задачу, тем более что передачу ключа нужно проводить довольно часто.

Решением этих проблем стал настоящий прорыв в криптографии — появление асимметричных криптосистем, которые не требовали передачи секретного ключа между сторонами. Началом принято считать работу, опубликованную Уитфилдом Диффи и Мартином Хеллманом в 1976 году под названием «Новые направления в современной криптографии».

Глоссарий

• Шифр
• Шифрование
• Расшифрование
• Шифратор
• Открытый текст
• Шифртекст
• Биграмма
• Ключ
• Шифр подстановки
• Многоалфавитный шифр
• Блочный шифр
• Полиграмный шифр
• Омофоническая замена
• Криптостойкость